What is Bayesian theory?
Bayesian is one of the two mutually exclusive sets of statistical fundamentals (the other one being Frequentist statistics) that can be used to model any statistical problem. Bayesians consider the parameter of interest to be subjective (a distribution of possibilities) described by a belief distribution that is updated on observing data.
On the other hand, frequentists consider the parameter of interest to be objective (one true point estimate) and rely on sampling multiple times to reach closer to the true parameter value. A deeper understanding and appreciation of the contrast between the two schools of thought require a thorough study of Bayesian vs Frequentist Statistics.
Bayesian enables an analyst to incorporate his belief in the research while estimating a parameter of interest. It provides a framework where an analyst can start with a prior belief and as more data is collected, his beliefs are updated as well. The integration of prior belief with available data is performed using Bayes’ theorem.
Suppose you wish to estimate the average American height. A statistician can have a prior belief that the height of an American would be spread around 50cm and 250cm. The study would involve measuring the height of several American individuals and as more observant are included in the study the spread would concentrate on measured average height.
The importance of Bayesian methodology
Bayesian methodologies are useful in parameter estimations when the data collection is costly for model building and the decision-making needs to happen on limited data. With large sample sizes, Bayesian methodologies often give results similar to the results produced by frequentist methods.
In hypothesis testing, it is much easier to interpret the results obtained from Bayesian compared to its counterpart Frequentist. In the Bayesian view, we work with a degree of certainty which is a probability that the true value of a parameter lies within the estimated range. This probability combines our knowledge of the value built on prior information with available data. This notion of probability makes it different from a Frequentist approach, wherein this degree of certainty is unknown. A hypothesis can then be chosen after a risk assessment based on this degree of certainty on the posterior estimate.
What is Bayesian inference?
Bayesian inference is all about updating your knowledge as new data comes in. As a Bayesian, you can rarely be certain about a result. But you can be confident, and depending upon the degree of confidence, you can make a decision. That’s it.
In Bayesian statistics, all observed and unobserved parameters in a statistical model are associated with probability distributions termed as the prior and data distributions. The typical Bayesian workflow involves the following three main steps:
- choose an appropriate prior distribution that captures available knowledge about a parameter in a statistical model. It is typically determined before data collection process;
- choose a likelihood function using the information about the available parameters and the observed data; and
- combine both the prior distribution and the likelihood function using Bayes’ theorem to obtain the posterior distribution of parameters.
The posterior distribution reflects one’s updated knowledge by combining prior knowledge with the observed data and is later used to conduct inferences.
In the case of an A/B test, by calculating the posterior distribution for each variant, we can express the uncertainty about our beliefs through probability statements. For example, we can ask “What is the probability that for a certain metric of interest, variant A will have a higher value than variant B?”. Interpretableoutput helps analysts to develop informative insights and share them with colleagues so they can make optimal decisions in complex business scenarios.
Strengths of Bayesian
- Provides a principled and natural way to combine domain knowledge with data – you can incorporate information from past experiments about a parameter and form a prior distribution for future experiments. With new observations, the posteriors of past experiments can work as the current prior to obtaining the new posterior.
- It provides interpretable answers. For instance – “There’s a probability of 0.9 that the true parameter will fall in a 90% credible interval.”
- It provides a natural framework for a wide range of parametric models like hierarchical models and missing data problems. MCMC, along with other numerical methods, provides a tractable computational design for all parametric models.
- No minimum data – Unlike Frequentist, no minimum data is required to work with a methodology built on Bayesian statistics. As the concept of uncertainty is already built into a Bayesian system, the metrics obtained from it remain valid.
Limitations of Bayesian
- Prior selection is not standardized – There is no well-defined way to choose a prior. It takes specialized skills to translate subjective prior beliefs into a mathematically formulated prior. Obtained results can be misleading if chosen prior don’t make sense.
- When the data is less, posterior distributions are heavily influenced by the priors. From a practical standpoint, it might invite debate if no consensus is made on the validity of the chosen prior.
- Bayesian methodologies often come with a high computational cost, especially when there are a large number of parameters involved. Although over the years many Bayesian methodologies have come up that are computationally efficient for certain use cases.
How does VWO use Bayesian?
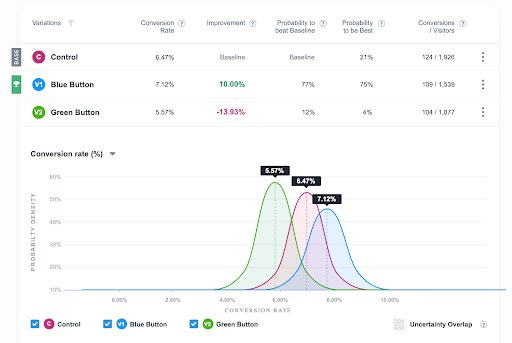
VWO is powered by a Bayesian statistics engine where the parameters of each variant in an A/B test are linked to a probability distribution. As data is observed in the test, these distributions are updated using Bayes’ theorem and we compute the decision metrics shown in our report using these updated distributions. Please refer to the VWO Whitepaper to understand the mathematics of our Bayesian modeling. You can also take a 30-day free trial to explore our reporting in detail.