What is a hypothesis?
A hypothesis is a proposed explanation or suggestion made by an analyst at the very start of any investigation. This proposition is built on past experiences/limited evidence available to the analyst even before any analysis is performed. It provides a concrete objective on what you can expect from the study.
Not all studies, however, have a hypothesis. Some are exploratory studies where the intent is to explore some area more thoroughly in order to develop some specific hypothesis or prediction that can be tested in future research.
Importance of hypothesis
A hypothesis helps in identifying the areas that should be focused on while solving a research problem. It provides an analytical framework to measure the validity and reliability of the research on the basis of evidence.
Research without a hypothesis is analogous to a sailor in the sea without a compass. A hypothesis provides a direction to research by providing quantifiable accuracy metrics. A good hypothesis can help the researcher to collect relevant data for the research and may lead to a good, reasonable conclusion.
Characteristics of a research hypothesis
A hypothesis must have the following characteristics-
- Should be clear and precise about what’s being assessed, who and what is involved, and very specific about the expected outcome, or else the inferences that are drawn on its basis cannot be taken as reliable.
- Should be capable of being tested. You must be able to collect observable data in a scientifically disciplined manner to assess whether it supports the hypothesis or not. There needs to be a way to support the claim.
- Should be falsifiable – there needs to be some identifiable way to test whether a hypothesis is false. If it is not possible to assess whether a claim is false, it’s not a hypothesis.
What is a hypothesis test?
In statistics, hypothesis testing is a procedure of testing whether or not the hypothesis is plausible. It is done to confirm our observation about the population using sample data, within the desired error level. Through hypothesis testing, we can determine whether we have enough statistical evidence to conclude if the proposed hypothesis about the population is true or not.
Most literature on hypothesis tests is built on frequentist statistics that generally involve two hypotheses. Suppose you wish to check if a relationship exists between two variables A and B in your study. A formal setup of a hypothesis test would involve creating two hypotheses –
- One that describes your prediction. A and B are related (you don’t care whether it’s a positive or negative relationship).
- One that describes all the other possible outcomes with respect to the hypothesized relationship. A and B are not related.
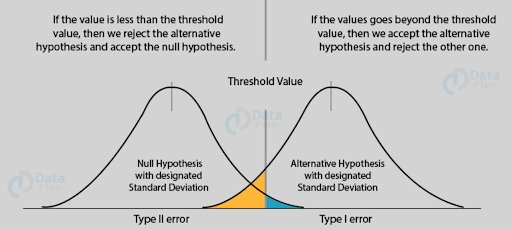
Most often we call the hypothesis we favor the alternate hypothesis(HA) and the hypothesis that describes all other possible outcomes as null hypothesis(H0).
Hypothesis testing can be analogous to a criminal trial where a jury must use evidence to decide between two possible truths, innocent (H0) or guilty (HA). Just as a jury is expected to assume that the defendant is innocent unless proven otherwise, the investigator should also assume no relationship unless there is strong evidence in favor of the alternate hypothesis. A jury’s verdict can either be guilty or not guilty, in which case a not-guilty verdict does not equal innocence. Rather, it indicates that the proofs are not sufficient to prove guilty. Similarly, an investigator can only reject H0 or fail to reject it; failure to reject does not prove that the null H0 is true, rather it means that the evidence does not strongly support the alternative hypothesis.
Bayesian hypothesis testing
Suppose that we need to decide between two hypotheses H0 and H1. In the Bayesian setting, we assume that we know prior probabilities of H0 and H1. That is, we know P(H0)=p0 and P(H1)=p1, where p0+p1=1. After running the experiment, we gather some data and obtain the posteriors using Bayes’ rule.
To decide between H0 and H1 we can compare the posterior probabilities of the two hypotheses and accept the one with the highest posterior probabilities.
At VWO, we use a bayesian hypothesis test to find the winner in an A/B test due to the following reasons –
- The metrics in the Bayesian framework are easy to read as compared to classical statistical tests.
- Posterior densities provide us with mathematical concepts intuitive to grasp and use in business as compared to p-values which are well known to be misleading countless times.
- Eventually, the concept of the Bayesian network allows us to conceive much more complex experiments and test multiple hypotheses by simply considering posterior distributions.
You can opt for a free trial with VWO or request a demo with our product experts to understand its reporting abilities in detail.