What is Simpson’s Paradox?
Simpson’s Paradox is a statistical phenomenon in which a trend or characteristic observed within individual data groups undergoes a reversal or disappearance when these groups are aggregated.
Let’s understand it through a simple hypothetical example.
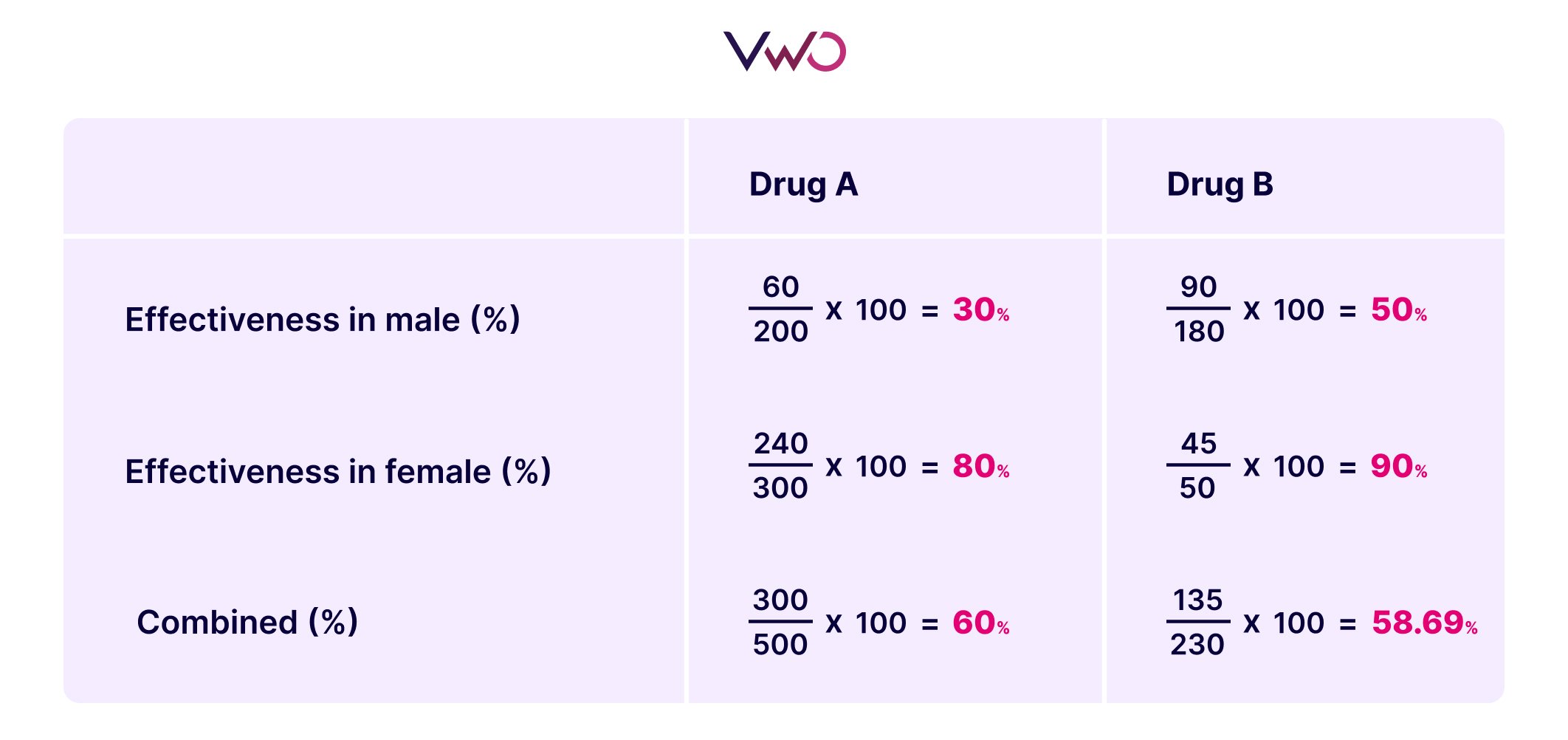
In a medical research facility, researchers evaluated the effectiveness of two drugs, labeled Drug A and Drug B, in improving a crucial health indicator. The overall results favored Drug A, indicating its superior performance.
However, when the data was dissected by gender, an interesting nuance emerged. Among men, Drug B surprisingly outperformed Drug A, while a similar trend was observed among women. Despite Drug A’s general superiority, the gender-specific analysis showcased distinct strengths for Drug B in both male and female cohorts.
The issue with Simpson’s Paradox is that it can be difficult for analysts to determine whether they should rely on insights from aggregated data or individual data groups. Simpson’s Paradox isn’t limited to any specific field; instead, it can manifest anywhere.
Why is Simpson’s Paradox important?
a. Highlights the pitfall of drawing misleading conclusions
Simpson’s Paradox highlights the pitfalls of drawing misleading conclusions from data without taking into account the variables involved. This oversight can be particularly consequential and worrisome in fields like medicine and scientific research, where precise data interpretation is crucial.
b. Emphasizes the need to control confounding variables
Confounding variables are factors that, while not the primary focus of a study, can significantly impact how we interpret the relationship between the main variables under investigation. These variables often sneak into the analysis and introduce biases or distortions, making it difficult to attribute any observed effects solely to the studied variables. Simpson’s Paradox highlights the importance of not only identifying these potential confounding variables but also actively taking steps to control for them in subsequent statistical analyses.
c. Showcases the complexity of the data at hand
The Simpson’s Paradox emphasizes the intricacy of interpreting data patterns. It shows that observed trends in subgroups may not hold when the data is combined, and vice versa. This serves as a reminder for analysts and researchers to avoid simplistic generalizations and adopt a more sophisticated and context-aware approach to data analysis.
How do you deal with Simpson’s Paradox?
a. Randomized sampling
In this process, the dataset is randomly divided into equal groups without favoring any specific data variable. The goal is to achieve a balanced distribution of confounding variables in both groups, minimizing the likelihood of their impact and preventing the occurrence of Simpson’s Paradox. Randomized sampling is mostly utilized when there is limited information available regarding confounding variables. It’s important to note, however, that randomized sampling is most effective with large samples, and the risk of uneven distribution of confounding variables increases with smaller sample sizes.
b. Blocking confounding variables
If you’ve pinpointed a confounding variable in a dataset through literature review and past experiment results, you can address the paradox by blocking those variables in the current dataset. For instance, if a previous dataset revealed a paradox related to male and female users, you can block gender as a variable in the current analysis. However, this approach becomes impractical when dealing with numerous confounding variables.
Simpson’s Paradox in A/B testing
The Simpson’s Paradox emerges when there’s inconsistency in traffic allocation during an A/B test. For instance, if you start with a 10-90 traffic split between variation and control on day 1, with 1000 visitors, and then, on day 2, you adjust the traffic to a 50-50 split for the variation and control with 600 visitors, you may encounter the Simpson’s Paradox in the dataset.
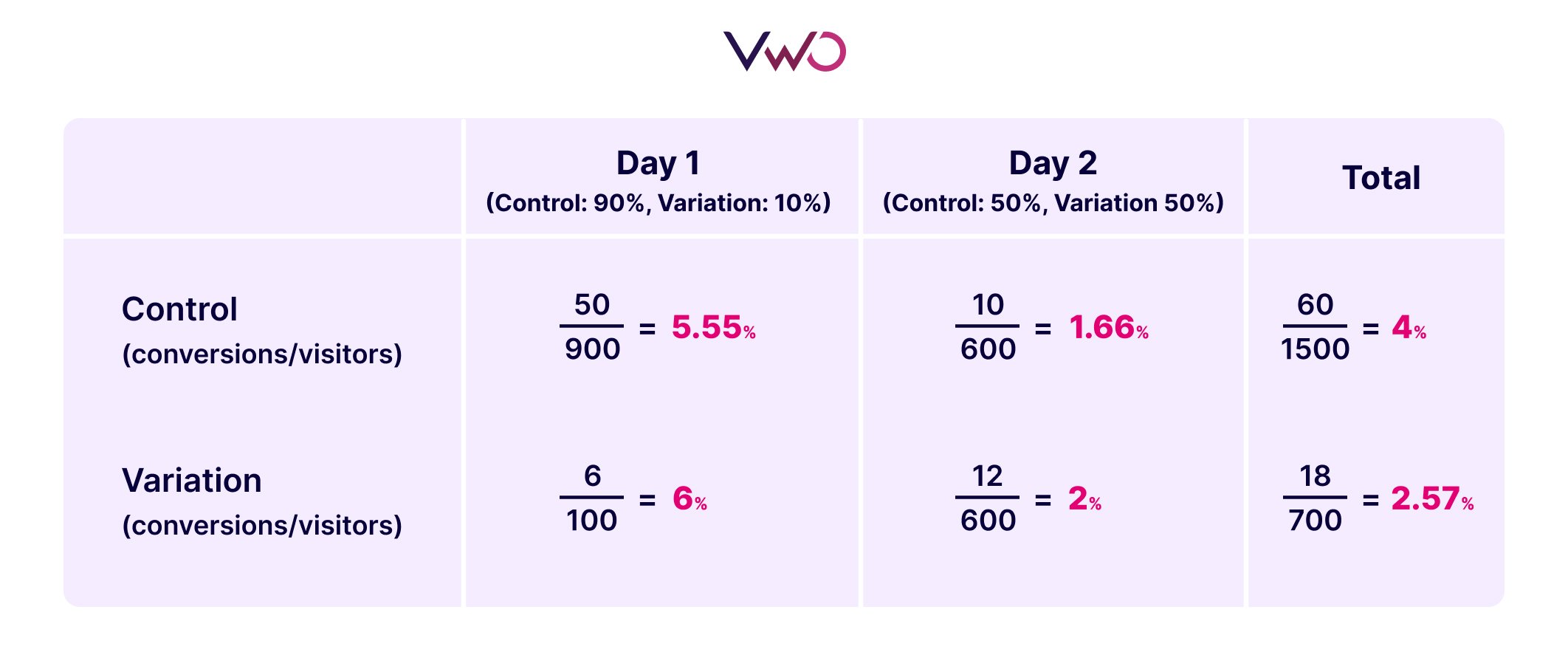
Across both days, the variation appears to boast a superior conversion rate. However, when you amalgamate the dataset, the control emerges as the winner. This discrepancy in results is a classic manifestation of Simpson’s Paradox, induced by the shift in traffic allocation between days. Such deceptive trends can be perilous, especially for large websites with significant financial stakes, potentially leading to misguided decisions. Hence, it’s always advisable to maintain consistent traffic allocation throughout the ongoing test to sidestep the occurrence of Simpson’s Paradox in the results.
Conclusion
Simpson’s Paradox rears its head in datasets influenced by confounding variables, making it crucial for businesses and analysts to stay vigilant and approach analysis with awareness. Remember, a thorough review of literature, past data analysis, and simulation can be instrumental in mitigating its effects. Being proactive in understanding and addressing potential confounding factors is key to ensuring accurate and reliable data interpretations.
Frequently Asked Questions (FAQs)
Simpson’s Paradox occurs when the analysis of data is oversimplified, leading to incorrect conclusions.
The solution to Simpson’s Paradox is identifying and negating the confounding variables.
Simpson’s Paradox manifests as a divergence in trends when data groups are amalgamated. In contrast, Berkson’s Paradox stems from selection bias in the sampling process, creating a correlation that may not exist in the broader population. Both paradoxes underscore the importance of careful consideration and nuanced analysis in statistical interpretation.