A/B Test Duration Calculator [Free Downloadable Excel]

In a previous post, I provided a downloadable A/B testing significance calculator (in excel). In this post, I will provide a free calculator which lets you estimate how many days you should run a test to obtain statistically significant results. But, first, a disclaimer.

There is no guarantee of results for an A/B test.

When someone asks how long should s/he run an A/B test, the ideal answer would be until eternity or till the time you get results (whichever is sooner). In an A/B test, you can never say with full confidence that you will get statistically significant results after running the test X number of days. Instead, what you can say is that there is an 80% (or 95%, whatever you choose) probability of getting a statistically significant result (if it indeed exists) after X number of days. But, of course, it may also be the case that there is no difference in the performance of control and variation so no matter how long you wait, you will never get a statistically significant result.

Download Free: A/B Testing Guide

So, how long should you run your A/B test?

Download and use the calculator below to find out how many visitors you need to include in the test. There are 4 pieces of information that you need to enter:

• The conversion rate of the original page
• % difference in conversion rate that you want to detect (if you want to detect even the slightest improvement, it will take much longer)
• Number of variations to test (more variations you test, more traffic you need)
• Average daily traffic on your site (optional)

Once you enter these 4 parameters, the calculator below will find out how many visitors you need to test (for 80% and 95% probability of finding the result). You can stop the test after you test those many visitors. If you stop before that, .you may end up getting wrong results.

A/B test duration calculator (Excel spreadsheet)

Click below to download the calculator:

Download A/B testing duration calculator.

Please feel free to share the file with your friends and colleagues or post it on your blog/twitter.

By the way, if you want to do quick calculations, we have a version of this calculator hosted on Google Docs (this will make a copy of the Google sheet into your own account before you can make any changes to it).

For all the people looking to calculate their calculation without the trouble of going through “sheets or documents”, we created a simple to use A/B testing duration calculator.

Download Free: A/B Testing Guide

How does the calculator work?

Ah! The million dollar calculator. Explaining how it works is beyond the scope of this post as it is too technical (needs a separate post). But, if you have got the stomach for it, below is a gist of how we calculate the number of visitors needed to get significant results.

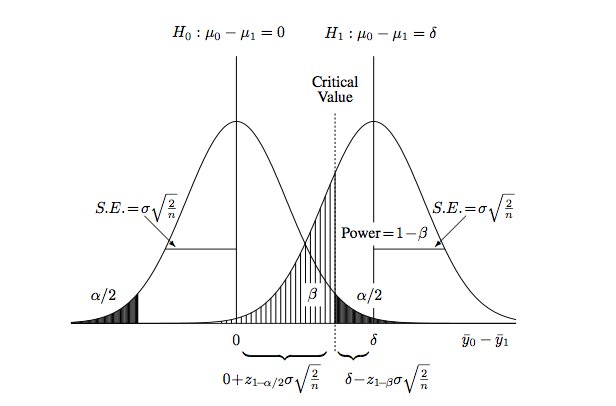
The graph above is taken from an excellent book called Statistical Rules of Thumb.

Luckily, the chapter on estimating sample size is available to download freely. Another excellent source to get more information on sample size estimation for A/B testing is Microsoft’s paper: Controlled Experiments on the Web: Survey and Practical Guide.

Hope you like the a/b test calculator and it helps your testing endeavours.