Bayesiano

¿Qué es el enfoque bayesiano?

El enfoque bayesiano es uno de los dos conjuntos mutuamente excluyentes de fundamentos estadísticos (el otro es la estadística frecuentista) que pueden utilizarse para modelar cualquier problema estadístico. Los bayesianos consideran que el parámetro de interés es subjetivo (una distribución de posibilidades) y lo describen mediante una distribución de creencias que se actualiza al observar datos. 

Por otro lado, los frecuentistas consideran que el parámetro de interés es objetivo (una única estimación puntual verdadera) y se basan en múltiples muestras para acercarse al valor real del parámetro. Para entender y apreciar bien la diferencia entre estas dos escuelas de pensamiento, es necesario estudiar en detalle la estadística bayesiana y la estadística frecuentista.

El enfoque bayesiano permite a un analista incorporar sus creencias en la investigación al estimar un parámetro de interés. Proporciona un marco en el que el analista puede comenzar con una creencia previa y, a medida que se recopilan más datos, sus creencias se actualizan. La integración de la creencia previa con los datos disponibles se realiza mediante el teorema de Bayes.

Supongamos que desea estimar la altura promedio de una persona estadounidense. Un estadístico podría tener la creencia previa de que la altura se encuentra entre 50 cm y 250 cm. El estudio consistiría en medir la altura de varias personas estadounidenses y, a medida que se incluyan más observaciones, esa distribución se concentraría en la media observada.

La importancia de la metodología bayesiana

Las metodologías bayesianas son útiles para la estimación de parámetros cuando la recopilación de datos es costosa para la construcción del modelo y las decisiones deben tomarse con datos limitados. Con tamaños de muestra extensos, las metodologías bayesianas suelen ofrecer resultados similares a los producidos por los métodos frecuentistas. 

En las pruebas de hipótesis, los resultados obtenidos mediante el enfoque bayesiano son mucho más sencillos de interpretar en comparación con su contraparte frecuentista. Desde la perspectiva bayesiana, trabajamos con un grado de certeza que es una probabilidad de que el valor real de un parámetro se encuentre dentro del rango estimado. Esta probabilidad combina nuestro conocimiento previo con los datos disponibles. Esta noción de probabilidad lo diferencia del enfoque frecuentista, en el cual ese grado de certeza es desconocido. Posteriormente, puede elegirse una hipótesis tras una evaluación de riesgos basada en este grado de certeza de la estimación posterior.

¿Qué es la inferencia bayesiana?

La inferencia bayesiana consiste en actualizar su conocimiento a medida que se incorporan nuevos datos. Como bayesiano, rara vez puede estar completamente seguro de un resultado. Pero puede tener confianza y, en función del grado de confianza, puede tomar una decisión. Eso es todo.

En la estadística bayesiana, todos los parámetros observados y no observados de un modelo estadístico están asociados a distribuciones de probabilidad denominadas distribución previa y distribución de datos. El flujo de trabajo típico en un enfoque bayesiano incluye los siguientes tres pasos principales:

• Elegir una distribución previa adecuada que refleje el conocimiento disponible sobre un parámetro en un modelo estadístico. Esta suele definirse antes del proceso de recopilación de datos; 
• Seleccionar una función de verosimilitud utilizando la información sobre los parámetros disponibles y los datos observados; y 
• Usar el teorema de Bayes para juntar la distribución previa y la función de verosimilitud y así obtener la distribución posterior de los parámetros.

La distribución posterior refleja el conocimiento actualizado, al combinar el conocimiento previo con los datos observados, y se utiliza posteriormente para realizar inferencias.

En el caso de un test A/B, al calcular la distribución posterior de cada variante, podemos expresar la incertidumbre sobre nuestras creencias a través de afirmaciones probabilísticas. Por ejemplo, podemos preguntar: «¿Cuál es la probabilidad de que, para una métrica determinada, la variante A tenga un valor superior al de la variante B?». Este tipo de resultados interpretables ayuda a los analistas a desarrollar conocimientos valiosos y compartirlos con sus colegas para que puedan tomar decisiones óptimas en escenarios empresariales complejos.

Fortalezas del enfoque bayesiano

• Ofrece una manera fundamentada y natural de combinar el conocimiento del dominio con los datos: se puede incorporar información de experimentos anteriores sobre un parámetro y formar una distribución previa para experimentos futuros. Con nuevas observaciones, las distribuciones posteriores de experimentos pasados pueden funcionar como distribuciones previas para obtener nuevas distribuciones posteriores.
• Proporciona respuestas interpretables. Por ejemplo: «Existe una probabilidad del 90 % de que el valor real del parámetro se encuentre dentro de un intervalo creíble del 90 %».

• Ofrece un marco natural para una amplia gama de modelos paramétricos, como los modelos jerárquicos y los problemas con datos faltantes. Los métodos MCMC, junto con otros métodos numéricos, permiten un diseño computacional viable para todos los modelos paramétricos.
• No requiere un tamaño mínimo de muestra: a diferencia del enfoque frecuentista, no se necesita una cantidad mínima de datos para aplicar una metodología basada en estadística bayesiana. Como el concepto de incertidumbre ya está integrado en el sistema bayesiano, las métricas obtenidas se mantienen válidas.

Limitaciones del enfoque bayesiano

• La selección de la distribución previa no está estandarizada: no existe una forma universalmente definida para elegir una distribución previa. Se requieren habilidades especializadas para traducir creencias previas subjetivas en una distribución previa formulada matemáticamente. Los resultados obtenidos pueden ser engañosos si la distribución previa seleccionada no tiene sentido.

• Cuando hay pocos datos, las distribuciones posteriores se ven muy influenciadas por las distribuciones previas. Desde un punto de vista práctico, esto puede generar debate si no hay consenso sobre la validez de la distribución previa elegida.

• Las metodologías bayesianas suelen tener un alto costo computacional, especialmente cuando se manejan muchos parámetros. No obstante, con el paso del tiempo, han surgido metodologías bayesianas más eficientes desde el punto de vista computacional para ciertos casos de uso.  

¿Cómo utiliza VWO el enfoque bayesiano?

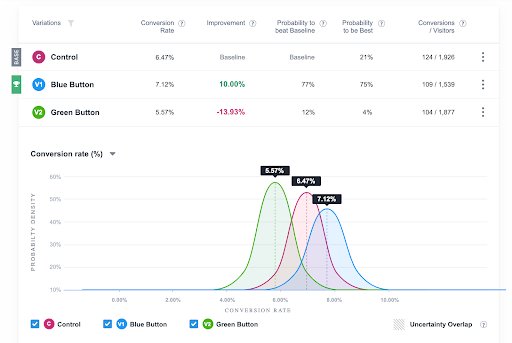
VWO funciona con un motor de estadísticas bayesianas en el que los parámetros de cada variante en un test A/B están vinculados a una distribución de probabilidad. A medida que se observan los datos en la prueba, estas distribuciones se actualizan utilizando el teorema de Bayes, y las métricas de decisión que mostramos en nuestros informes se calculan a partir de estas distribuciones actualizadas. Consulte el whitepaper de VWO para comprender las matemáticas de nuestro modelo bayesiano. También puede solicitar una prueba gratuita de 30 días para explorar nuestros informes en detalle.