A/B Test Statistical Significance Calculator
Want to run an online A/B test? Calculate its significance with our Bayesian-powered calculator built for experimentation, CRO, and UX Optimization.
P-Value
(Desde 0-1)0.334
Significance
No
What is statistical significance?
Statistical significance quantifies whether a result obtained is likely due to chance or some factor of interest. You can utilize a significance calculator to confidently evaluate and interpret your results. The data-driven approach empowers you to make informed decisions for optimization and ultimately achieve your desired outcomes.
Different approaches to calculate statistical significance
The two commonly used approaches are Frequentist and Bayesian, which power different test statistics calculators. Here is a brief information on each.
Frequentist
Frequentist statistics involves examining the frequency of events. It looks at how often something happens in a given situation.
Bayesian
Bayesian statistics is all about changing your opinion. It starts with an initial belief called the prior, which comes from domain expertise. Then, you gather evidence to support or challenge that belief. After examining the evidence, your opinion should be updated based on the new information you’ve acquired.
How do we calculate statistical significance?
Here is how you can calculate statistical significance using the Frequentist and Bayesian approaches.
Frequentist approach
The Frequentist approach to statistical significance is based on the p-value. To determine the p-value using the Frequentist approach, you will need the following key pieces of information:
- The mean difference between the two hypotheses
- The standard deviation of the difference between the two hypotheses
- The sample size of each hypothesis
Once you have gathered this necessary data, you can easily compute the p-value using a significance testing tool or significance level calculator. If the p-value you get is 0.05, the probability of the variation is 5%.

Bayesian Approach
In this, you do statistical significance calculation through posterior probability. The posterior probability considers the available data and represents the probability of hypothesis A or B being true. The approach takes into account both prior beliefs and the evidence observed in the data.
To calculate the posterior probability, Bayes' theorem is employed. Bayes' theorem is a mathematical formula that combines the prior probability of a hypothesis with the likelihood of the data to derive the updated or posterior probability.
A posterior probability of greater than 95% is considered to be strong evidence in favor of the hypothesis.
Know more about our Bayesian approach in the article series we created on Bayesian A/B testing at VWO.

¿Por qué usamos estadística bayesiana?
Informes de tests intuitivos
At VWO, we recognize that non-statistical users often misinterpret the frequentist p-value as a Bayesian posterior probability, which leads to incorrect conclusions about the superiority of one variation over another. To address this issue, we developed the industry's first Bayesian statistical engine.
Our Bayesian statistical engine provides users with easily understandable results, eliminating the risk of making mistakes while conducting A/B tests on revenue or other crucial key performance indicators (KPIs). By adopting a more intuitive approach, we ensure that our users obtain accurate insights from our A/B test statistical significance calculator.
With our solution, you can have confidence in the statistical significance of your results, making informed decisions to optimize your testing, revenue generation, and overall user experience. Say goodbye to misinterpretations and embrace the power of the Bayesian A/B test calculator for reliable and actionable A/B testing outcomes.

Get clear comparisons against the baseline
Identify if variations outperform, match, or fall below the baseline with our advanced stats engine. Results are declared at a 95% probability threshold. Detailed graphs offer clear insights for effective decision-making.
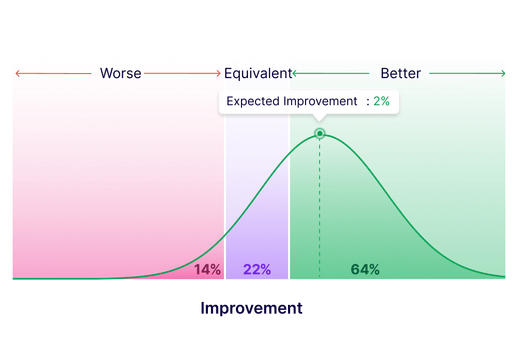
Resultados procesables, más rápidos
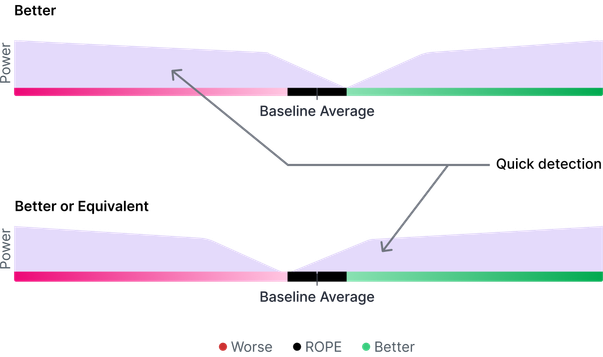
VWO offers two testing objectives, "Better" and "Better or Equivalent," both built on ROPE (Region of Practical Equivalence), which offers asymmetric power in tests.
The "Better" objective helps you quickly identify underperforming variations. This speeds up your evaluations and lets you focus on implementing successful changes faster.
The "Better or Equivalent" objective delivers quicker experiment results when you're looking for either an improvement over the baseline or a performance that's essentially the same.
Preguntas frecuentes
La hipótesis nula establece que no existe diferencia entre el control y la variación. Esto significa que la tasa de conversión de la variación será similar a la tasa de conversión del control.
El valor p se define como la probabilidad de obtener resultados al menos tan extremos como los observados, teniendo en cuenta que la hipótesis nula es correcta (siendo la hipótesis nula en A/B testing la idea de que la variación y el control son lo mismo).
La significancia estadística cuantifica si un resultado obtenido se debe probablemente al azar o es fruto de un factor relevante. Cuando se establece que un descubrimiento es estadísticamente significativo, esto quiere decir que puedes tener la certeza de que la diferencia es real, y no que simplemente tuviste suerte (o mala suerte) a la hora de escoger la muestra.
El poder estadístico es la probabilidad de detectar un efecto cuando dicho efecto es real. Por lo tanto, un poder estadístico del 80 % significa que de 100 tests en los que las variaciones son diferentes, hay 20 en los que las variaciones son lo mismo y, como consecuencia, no existe efecto.