Recently, I published an A/B split testing case study where an eCommerce store reduced the bounce rate by 20%. Some of the blog readers were worried about the statistical significance of the results. Their main concern was that a value of 125-150 visitors per variation is not enough to produce reliable results. This concern is a typical by-product of having superficial knowledge of statistics which powers A/B (and multivariate) testing. I’m writing this post to provide an essential primer on the mathematics of A/B split testing so that you never jump to a conclusion on the reliability of test results simply on the basis of the number of visitors.
Download Free: A/B Testing Guide
What exactly goes behind A/B split testing?
Imagine your website as a black box containing balls of two colors (red and green) in unequal proportions. Every time a visitor arrives on your website, he takes out a ball from that box: if it is green, he makes a purchase. If the ball is red, he leaves the website. This way, essentially, that black box decides the conversion rate of your website.
A key point to note here is that you cannot look inside the box to count the number of balls of different colors to determine the true conversion rate. You can only estimate the conversion rate based on different balls you see coming out of that box. Because conversion rate is an estimate (or a guess), you always have a range for it, never a single value. For example, mathematically, the way you describe a range is:
“Based on the information I have, 95% of the times conversion rate of my website ranges from 4.5%-7%.”
As you would expect, with more visitors, you get to observe more balls. Hence, your range gets narrower, and your estimate starts approaching the true conversion rate.
The maths of A/B split testing
Mathematically, the conversion rate is represented by a binomial random variable, which is a fancy way of saying that it can have two possible values: conversion or non-conversion. Let’s call this variable p. Our job is to estimate the value of p, and for that, we do n trials (or observe n visits to the website). After observing those n visits, we calculate how many visits resulted in a conversion. That percentage value (which we represent from 0 to 1 instead of 0% to 100%) is the conversion rate of your website.
Now imagine that you repeat this experiment multiple times. It is very likely that, due to chance, every single time, you will calculate a different value of p. Having all (different) values of p, you get a range for the conversion rate (which is what we want for the next step of analysis). To avoid doing repeated experiments, statistics has a neat trick in its toolbox. There is a concept called standard error, which tells how much deviation from the average conversion rate (p) can be expected if this experiment is repeated multiple times. The smaller the deviation, the more confident you can be about estimating the true conversion rate. For a given conversion rate (p) and the number of trials (n), the standard error is calculated as:
Standard Error (SE) = Square root of (p * (1-p) / n)
Without going much into details, to get a 95% range for conversion rate multiply the standard error value by 2 (or 1.96 to be precise). In other words, you can be sure with 95% confidence that your true conversion rate lies within this range: p % ± 2 * SE
(In VWO, when we show the conversion rate range in reports, we show it for 80%, not 95%. So we multiply standard error by 1.28).
Apart from standard error, while doing A/B testing, you would have to take into consideration Type I & Type II errors.
Download Free: A/B Testing Guide
What does it have to do with reliability of results?
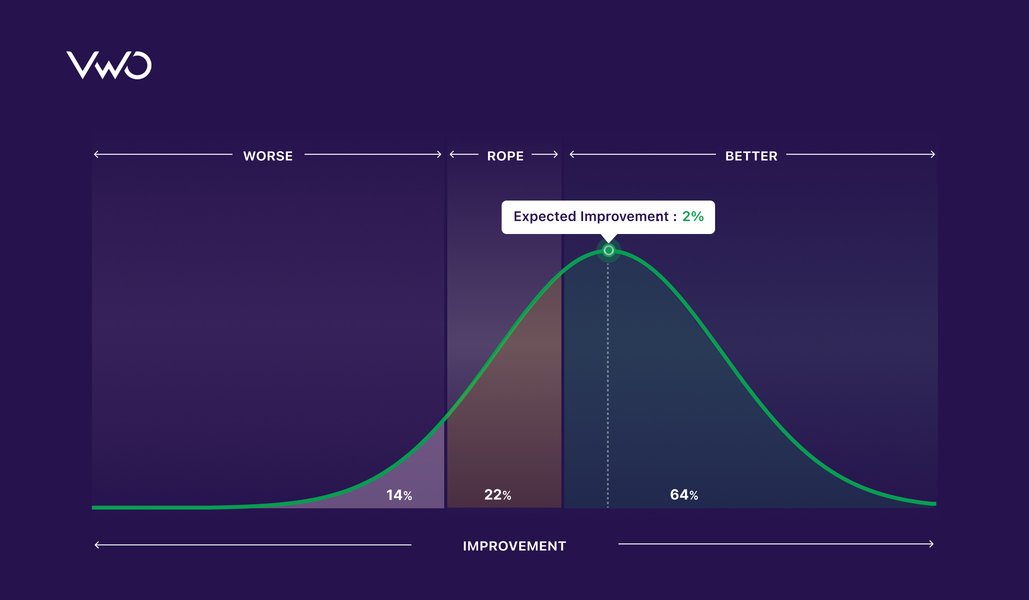
In addition to calculating the conversion rate of the website, we also calculate a range for its variations in an A/B split test. Because we have already established (with 95% confidence) that the true conversion rate lies within that range, all we have to observe now is the overlap between the conversion rate range of the website (control) and its variation. If there is no overlap, the variation is definitely better (or worse if the variation has a lower conversion rate) than the control. It is that simple.
As an example, suppose control conversion rate has a range of 6.5% ± 1.5% and a variation has a range of 9% ± 1%. In this case, there is no overlap, and you can be sure about the reliability of the results.
Do you call all that math simple?
Okay, not really simple, but it is definitely intuitive. To save the trouble of doing all the math by yourself, either use a tool like VWO Testing which automatically does all the number crunching for you. Or, if you are doing a test manually (such as for Adwords), use our free A/B split test significance calculator.
So, what is the take-home lesson here?
Always, always, always use an A/B split testing calculator to determine the significance of results before jumping to conclusions. Sometimes you may discount significant results as non-significant solely on the basis of the number of visitors. Sometimes you may think results are significant due to the large number of visitors when in fact they are not.
You really want to avoid both scenarios, don’t you?