Hipótesis

¿Qué es una hipótesis?

Una hipótesis es una explicación o suposición planteada por un analista al inicio de cualquier investigación. Esta propuesta se basa en experiencias previas o en evidencia limitada disponible, incluso antes de realizar cualquier análisis. Proporciona un objetivo concreto sobre lo que puedes esperar del estudio. 

Sin embargo, no todos los estudios parten de una hipótesis. Algunos son estudios exploratorios, cuyo propósito es investigar un área con mayor profundidad para, más adelante, formular una hipótesis específica o una predicción que se pueda poner a prueba en futuras investigaciones.

Importancia de la hipótesis

Una hipótesis te ayuda a identificar las áreas en las que deberías centrarte al abordar un problema de investigación. Proporciona un marco analítico que permite medir la validez y fiabilidad del estudio en función de la evidencia recopilada.

Hacer investigación sin una hipótesis es como navegar en el mar sin brújula. Una hipótesis aporta dirección a la investigación al ofrecer métricas cuantificables de precisión. Una hipótesis acertada puede ayudarte a recopilar datos relevantes para el estudio y puede conducir a una conclusión sólida y razonada.

Características de una hipótesis de investigación

Una hipótesis debe cumplir con las siguientes características:

1. Debe ser clara y precisa: tiene que especificar qué se está evaluando, quiénes o qué están involucrados y cuál es el resultado esperado. Si no es específica, las inferencias obtenidas no serán fiables.
2. Debe poder ponerse a prueba: tienes que poder recopilar datos observables de forma científica para evaluar si apoyan o no la hipótesis. Debe existir una manera concreta de validar la afirmación. 
3. Debe ser falsable: tiene que haber una forma identificable de demostrar que la hipótesis es falsa. Si no es posible comprobar si una afirmación puede ser refutada, entonces no es una hipótesis válida.

¿Qué es una prueba de hipótesis?

En estadística, una prueba de hipótesis es un procedimiento que permite comprobar si una hipótesis es plausible. Se realiza para confirmar nuestras observaciones sobre una población usando datos muestrales, dentro de un margen de error aceptable. A través de este proceso, podemos determinar si tenemos suficiente evidencia estadística para concluir si la hipótesis planteada sobre la población es verdadera o no.

La mayoría de la literatura sobre pruebas de hipótesis se basa en la estadística frequentista, que generalmente implica el planteamiento de dos hipótesis. Supongamos que quieres comprobar si existe una relación entre dos variables, A y B, en tu estudio. Una estructura formal de prueba de hipótesis incluiría: 

• Una hipótesis que representa tu predicción: A y B están relacionados (sin importar si es una relación positiva o negativa). 
• Otra hipótesis que representa todas las demás posibilidades: A y B no están relacionados.

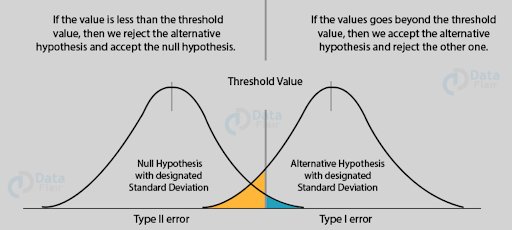
Normalmente, se denomina hipótesis alternativa (HA) a la que queremos demostrar, y hipótesis nula (H₀) a la que representa la ausencia de relación o efecto. 

La prueba de hipótesis puede compararse con un juicio penal, donde un jurado debe decidir entre dos verdades posibles: inocente (H₀) o culpable (HA). Al igual que se espera que un jurado asuma que el acusado es inocente hasta que se demuestre lo contrario, quien realiza la prueba estadística debe asumir que no hay relación (hipótesis nula) a menos que haya evidencia sólida a favor de la hipótesis alternativa.  Un jurado solo puede emitir un veredicto de culpable o no culpable. Un veredicto de “no culpable” no implica que el acusado sea inocente, sino que no se presentó suficiente prueba para condenarlo. De manera similar, un investigador solo puede rechazar la H₀ o no rechazarla; el hecho de no rechazarla no significa que la H₀ sea verdadera, sino que la evidencia no apoya de forma contundente la hipótesis alternativa.

Pruebas de hipótesis bayesianas

Supongamos que necesitamos decidir entre dos hipótesis: H₀ y H₁. En un enfoque bayesiano, se parte del supuesto de que conocemos las probabilidades previas de cada hipótesis: P(H₀) = p₀ y P(H₁) = p₁, donde p₀ + p₁ = 1.  Tras realizar el experimento, se recopilan los datos y se calculan las distribuciones posteriores mediante la regla de Bayes. 

Para decidir entre H₀ y H₁, se comparan las probabilidades posteriores y se acepta la hipótesis con mayor probabilidad posterior.   

En VWO, usamos la prueba de hipótesis bayesiana para determinar el ganador en un A/B testing por las siguientes razones: 

• Las métricas del enfoque bayesiano son más fáciles de interpretar que las pruebas estadísticas clásicas.
• Las densidades posteriores ofrecen conceptos matemáticos más intuitivos y aplicables al negocio, en comparación con los valores p, que han demostrado ser confusos en múltiples ocasiones.
• El uso de redes bayesianas nos permite concebir experimentos mucho más complejos y poner a prueba múltiples hipótesis simultáneamente, considerando únicamente sus distribuciones posteriores.

¿Quieres probarlo? Puedes solicitar una demo personalizada con nuestros expertos en producto o activar una prueba gratuita con VWO para explorar a fondo sus capacidades de análisis y reporting.