The famous Monty Hall problem and what it has to do with A/B testing

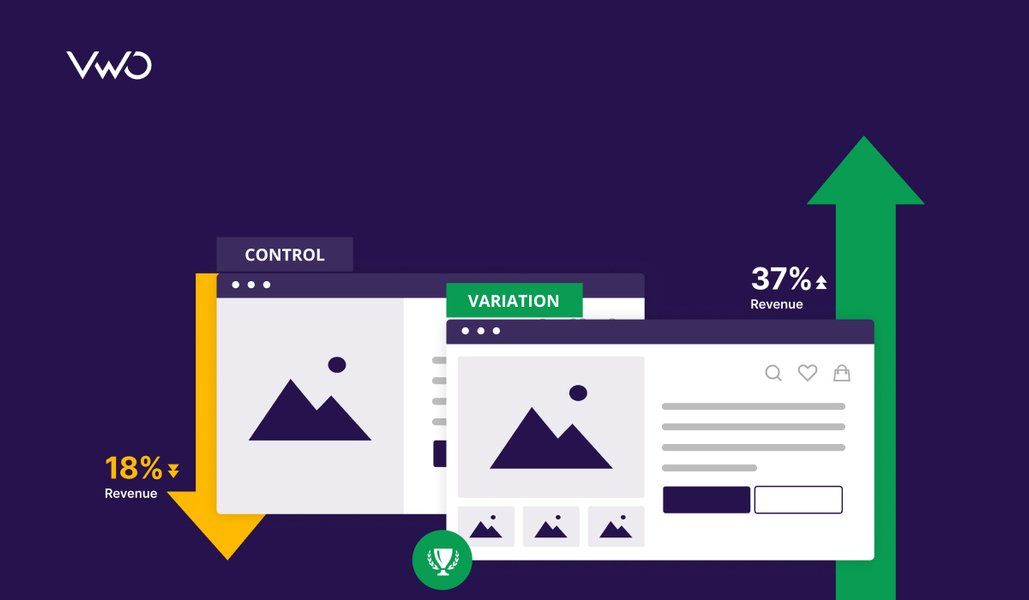
The feedback I received on “How large should your A/B test sample size be?” inspired me to write this new post. The goal is to demonstrate that indeed probability can be a tough and even counterintuitive concept, but once understood and applied it can yield tremendous advantages.

Download Free: A/B Testing Guide

This post is about what has come to be known as the ‘Monty Hall Problem’.

This is the situation: you are a contestant on a game show and the host offers you three doors to choose from. He informs you that behind two doors are cheap items and behind one is the real prize.

You choose a door, say, door A, and instead of opening this door to reveal its contents, the host opens one of the two doors you didn’t pick, say, door B. Important detail: he always picks a door with a cheap item. He then asks, do you want to stick to your choice or switch to the other closed door, door C.

What usually follows are sighs of doubt, thinking, looking for cues from the host and finally the answer, yes, I would like to change, or, no, I will not change to the other door.

What is the wise move? Should you switch doors or not? Many people say ‘how would that help? Probability stays as it was: 1/3’ or ‘now we have two closed doors each with a probability of ½, but changing doesn’t help anything’.

If this dilemma is new to you and you’re challenged to figure this out, stop reading now. Otherwise please continue.

The answer is, yes, you should switch, because that doubles your chances of winning the real prize.

It is non-intuitive, but actually very simple: suppose the above red door is the door with the real prize.

If you choose this red door, the host will open either of the green doors and you switch to the other green door. Result: No Prize.

If you choose the middle green door, the host will open the left green door and you switch to the red door. Result: You Win The Prize.

If you choose the left green door, the host will open the middle green door and you switch to the red door. Result: You Win The Prize.

So by changing doors you double the probability of winning the prize from 1/3 to 2/3.

If you don’t switch, the probability remains 1/3.

If you are not convinced yet, play the game with a colleague as the host and try thirty times with and thirty times without switching. Then count the number of successes in each condition.

There are other ways to solve this problem, but this one works for me.

Simple and demonstrably counterintuitive. Yet if you take the time to figure out the logic you will greatly benefit in similar situations in the future.

Now, what is the comparison between this problem and the sample size blog?

Well, both are about the usage of additional information to optimize decision making.

The mere additional fact of opening a door without the prize by the host, allows you improve your chances of winning the prize greatly.

Suppose you had a chance to improve your business by using additional information.

Taking into account the lesser-known concept of ‘power’ along with the better-known concept of ‘reliability’ – both probabilities – when establishing desired sample size as described in “How large should your A/B test sample size be?” actually adds information that allows you to structurally improve your decision making in A/B testing and Multivariate testing.

Download Free: A/B Testing Guide

Two metaphors:

What would be the use of choosing sample sizes that are so small it would be virtually impossible to find significant results, assuming the supposed effect really exists? It’s like flying from Amsterdam to Paris with too little fuel. Odds are you will have to land in Reims, meaning you did not reach your destination. Only in rare circumstances would you be lucky enough to make it to Paris. This is about too little power due to the small sample size.

What would be the use of choosing strict reliability if the sample size can’t be stretched and again it would be impossible to find significant results, given the existence of that effect? That’s like driving through Paris while attempting to avoid getting even the smallest scratch on the bumpers. You can try hard, but you will not get very far or park anywhere since under those circumstances, it would be virtually impossible. This is about too little power due to strict reliability.

A business case:

A company wanted to test a new loyalty program intended to reduce churn amongst its best customers. Churn was 5.0 % and they want to lower it to 4.5 %. A reduction of 10%. They decided to use two samples of 5,000 each. One for the test, and the other for control.

The test failed. There was an impressive reduction of 8% (control 5.1%, test 4.7%), but this was not statistically significant. Alright, this is always possible. But if we go back to the assumptions at the start of the test, we can calculate that we would have needed about two times 22,000 observations to have a fair chance to demonstrate what was assumed true. Too little fuel, and they didn’t make it to Paris.

What makes this so bad is that they learned the wrong lesson. Rather than understanding that their test may have failed because it wasn´t correctly carried out, they believe that the program doesn’t work.

For analysts who see relatively small effects in their tests and use small sample sizes, count the times the marketer says, “As predicted the test variation did better than the control, yet you tell me it is not true” and compare this to the number of tests that also show non-significant results where the prediction of the marketer is reversed in the test: “contrary to prediction control did better than test, but not significant”. If the occurrence of the former is significantly greater than the latter, your testing needs tuning.

Adjust the sample size to reach an acceptable power, take more fuel, or, if that is not possible, lower the reliability of the test, and accept more scratches on the bumper.

It´s up to you to decide which is worse: saying the program does work, when it actually does not, versus, saying the program does not work, when it actually does. In the first scenario, the loyalty program gets implemented, but it doesn’t help reduce churn. How costly is that scratch? In the second scenario, the loyalty program will not be implemented, whereas it would have been a success. How costly is that failure to arrive at a destination? Weigh these two options. If you cannot reach an acceptable compromise, don’t do the test.

Different goals, different weighing. If you have to choose between a smaller or a bigger button, you might say, ” If after the test we believe a bigger button to be better than the smaller version, but they actually converse the same, that would not really be bad” – unimportant scratch – and also say, “if after the test we believe that the bigger button is equally good as the smaller, whereas the bigger button actually converses better, that would actually be very regrettable”  – important failure to reach the destination – and visitor sizes are simply limited, we could choose to go easy on reliability – the higher probability to get a scratch – but be strict on power – the higher probability to arrive on destination -.

Of course, everybody is entitled to follow rules of thumb and, as said earlier, VWO provides excellent ones, so there is really no reason to hesitate using these. But if in your company you are the decision maker using statistical tests, it would be a comfortable thought if you could defend those choices based on your own knowledge.

Follow the HackerNews discussion here.

Edit: Here’s the game by The New York Times. You can see the original on this page.