¿Qué es un error tipo II?
Supongamos que una empresa quiere aumentar el número de usuarios que adoptan un nuevo producto.
La empresa formula una hipótesis para ofrecer una prueba gratuita que puede incentivar a los usuarios a probar el producto y evaluarlo según sus necesidades. Para validar esta hipótesis, la empresa realiza un test A/B entre dos estrategias: ofrecer una prueba gratuita y no ofrecerla. Después de ejecutar el experimento durante un tiempo determinado, el resultado es estadísticamente no significativo. Dado que el test no ofrece evidencia sólida a favor de la hipótesis planteada, esta se rechaza y la empresa decide no implementar la prueba gratuita.
Ahora bien, supongamos que en realidad el resultado fue erróneo y que ofrecer pruebas gratuitas sí aumentaba el número de usuarios del producto. En ese caso, el test habría cometido un falso negativo, también conocido como error tipo II. Si una prueba A/B o multivariante indica que no hay diferencia estadística cuando en realidad sí la hay entre las variaciones, se comete un error tipo II.
En términos científicos, durante el proceso de test de hipótesis, se comete un error tipo II cuando el test no rechaza la hipótesis nula (que representa la ausencia de efecto o diferencia), aunque esta sea falsa y debería haber sido rechazada. Una hipótesis nula se define antes de iniciar un test A/B o una prueba multivariante (MVT) y representa que no existe ninguna diferencia significativa entre las variaciones que se están probando.
¿Por qué es importante entender los errores tipo II?
Cada error tipo II representa una oportunidad perdida para innovar y, potencialmente, podría haber generado un aumento en la tasa de conversión a largo plazo. Un número elevado de errores tipo II puede hacer que se descarten muchas ideas con potencial real, impidiendo el crecimiento del negocio.
Causas de los errores tipo II
Los errores tipo II están inversamente relacionados con la potencia estadística de un test. Una alta potencia estadística implica una baja probabilidad de cometer un error tipo II. La potencia estadística es la probabilidad de que un test detecte una diferencia real en la tasa de conversión entre variaciones, si dicha diferencia existe.
La potencia estadística, junto con la diferencia mínima significativa que deseas detectar, determina el tamaño de muestra necesario para el test. Cuanto mayor sea la potencia estadística y menor sea el efecto que deseas detectar, mayor será la muestra requerida y, por tanto, más larga será la duración del test.
Un test queda infraalimentado (underpowered) si se detiene antes de alcanzar el tamaño de muestra necesario, lo que incrementa la probabilidad de errores tipo II. Esto puede impedir detectar resultados verdaderamente positivos, incluso cuando hay diferencias sustanciales.
En pruebas A/B o tests multivariantes (MVT), existe un equilibrio entre la precisión estadística y la duración del experimento. En función de la diferencia en la tasa de conversión que sea estratégicamente relevante para tu negocio y del nivel de potencia deseado, puedes calcular el tamaño de muestra más adecuado para tu test.
Representación gráfica de los errores tipo II
A continuación, se muestra una representación visual de un modelo de hipótesis nula frente a un modelo de hipótesis alternativa:
- El modelo nulo representa la probabilidad de obtener todos los posibles resultados si se repitiera el estudio con nuevas muestras y la hipótesis nula fuera verdadera en la población.
- El modelo alternativo muestra la probabilidad de obtener los resultados si se repitiera el estudio y la hipótesis alternativa fuera la verdadera.
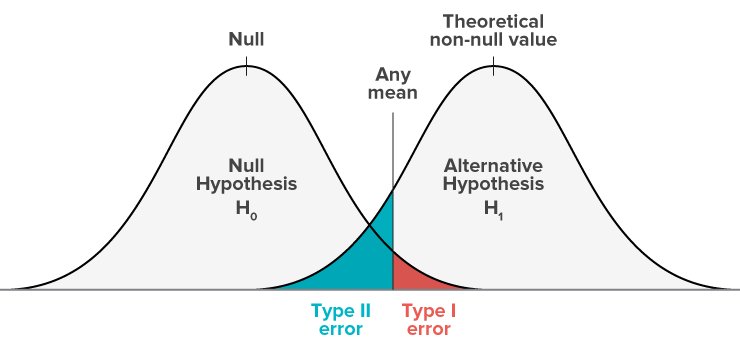
La zona sombreada representa la región crítica. Si los resultados de tu test caen dentro de esta región azul, se consideran estadísticamente no significativos y, por tanto, no se rechaza la hipótesis nula. Sin embargo, si en realidad la hipótesis nula es falsa, esta conclusión sería incorrecta: estarías cometiendo un falso negativo, es decir, un error tipo II.
La relación entre el error tipo I y el error tipo II
En estadística, las tasas de error tipo I y error tipo II están relacionadas y se influyen mutuamente. El error tipo I depende del nivel de significancia establecido para la prueba, y este a su vez afecta la potencia estadística del test.
Como la potencia estadística es inversamente proporcional a la tasa de error tipo II, existe un compromiso entre ambos tipos de error:
- Un nivel de significancia bajo reduce el riesgo de cometer un error tipo I, pero aumenta el riesgo de cometer un error tipo II.
- Un test con alta potencia estadística reduce la probabilidad de error tipo II, pero puede aumentar la del error tipo I.
Ambos errores se producen en la zona de superposición de las distribuciones de las dos hipótesis. En una representación gráfica, el área roja suele representar alfa (error tipo I) y el área azul, beta (error tipo II).
Por tanto, al fijar el nivel de significancia (error tipo I), también estás influyendo indirectamente en el tamaño del error tipo II.
¿Cómo controlar el error tipo II?
La forma más eficaz de reducir el riesgo de cometer un error tipo II es aumentar la potencia estadística del test. Para ello, existen varias estrategias:
- Aumentar el tamaño de muestra
Cuanto mayor sea el número de muestras, mayores serán las probabilidades de detectar una diferencia real, lo que incrementa la potencia del test.
- Aumentar el umbral de significancia
La mayoría de los tests estadísticos usan un nivel de significancia del 0,05 para determinar si un resultado es estadísticamente significativo. Si aumentas ese umbral (por ejemplo, a 0,10), incrementas la probabilidad de rechazar la hipótesis nula, lo que reduce los errores tipo II.
Sin embargo, esto también incrementa el riesgo de cometer errores tipo I. Por eso es esencial evaluar el impacto de ambos errores en tu contexto de negocio y establecer un nivel de significancia adecuado.
En VWO utilizamos dos métricas clave para la toma de decisiones en experimentación: Probability to be the Best (PBB) y Absolute Potential Loss (PL). Probability to be the Best (PBB): mide la probabilidad de que una variación sea mejor que las demás. Establecer un umbral más alto de PBB puede ayudarte a reducir la probabilidad de cometer errores tipo II, aumentando así la confiabilidad de tus decisiones.
¿Quieres profundizar en cómo VWO puede ayudarte a minimizar este tipo de errores y mejorar la toma de decisiones en tus tests? Solicita una demo gratuita o prueba VWO sin compromiso y descubre cómo optimizar tu proceso de experimentación con datos sólidos.