¿Qué es un error tipo I?
Imagina que un negocio de eCommerce quiere aumentar sus ventas. Formulan la hipótesis de que optimizando el diseño de la página de producto podrían mejorar la tasa de finalización del checkout, lo que incrementaría las compras.
Para validar esta hipótesis, realizan un test A/B comparando dos diseños y miden la tasa de clic en el botón de checkout. Según el enfoque de test de hipótesis de un A/B test, si tras un periodo de experimentación los resultados muestran un resultado estadísticamente significativo a favor del nuevo diseño, la hipótesis se considera verdadera.
Ahora bien, supongamos que los resultados fueron erróneos y que en realidad no existía diferencia entre los dos diseños. En ese caso, el test habría cometido un falso positivo o error tipo I. Si una prueba A/B o multivariante indica que hay diferencia estadística cuando en realidad no la hay entre las variaciones, se comete un error tipo I.
En términos científicos, un error tipo I ocurre cuando en un test de hipótesis se rechaza la hipótesis nula (que representa que no hay efecto), aunque en realidad esta es cierta y no debería haberse rechazado. La hipótesis nula se define antes de iniciar un test A/B o un test multivariante (MVT) y representa que no hay diferencia entre las variaciones evaluadas.
De forma formal: En un test A/B, si ambas variaciones son similares y no afectan de forma diferente a la métrica evaluada, puede ocurrir un error al rechazar la hipótesis nula. Si se detecta una diferencia estadística que en realidad no existe, se produce un error tipo I.
¿Por qué es importante entender los errores tipo I?
Si después de un A/B test concluyes incorrectamente que la variación B es la ganadora y la implementas para todo el tráfico, esta decisión equivocada podría perjudicar la tasa de conversión y suponer una pérdida de ingresos para el negocio. Por eso, entender los errores tipo I al realizar A/B tests es clave para:
- Estimar el riesgo de llegar a una conclusión errónea.
- Realizar experimentación de forma científica y rigurosa.
¿Qué causa un error tipo I?
Al realizar un test estadístico, siempre existe la posibilidad de cometer un error tipo I, ya que las estimaciones se realizan sobre una muestra limitada de datos. Un test estadístico no garantiza tomar siempre la decisión correcta, sino la decisión correcta la mayoría de las veces. Por ello, una metodología de testing debe evaluarse en función de su capacidad para limitar los errores dentro de un margen aceptable.
Los errores tipo I suelen deberse principalmente a dos causas:
- Azar: En un test de hipótesis, el analista trabaja solo con una parte reducida de la población de datos para hacer estimaciones. Por tanto, existe la posibilidad de que en determinados casos las muestras recogidas no representen adecuadamente a la población real, lo que puede conducir a conclusiones incorrectas.
- Finalizar el test antes de tiempo: En el testing de hipótesis frecuentista, se espera que el test se realice una vez se ha alcanzado el tamaño de muestra deseado para el estudio. Sin embargo, en muchos casos los tests se interrumpen en cuanto el p-valor baja del umbral definido, lo que provoca un aumento de la tasa de falsos positivos.
Representación gráfica de la tasa de error tipo I
A continuación, se muestra una representación visual de un modelo de hipótesis nula frente a un modelo de hipótesis alternativa:
- El modelo nulo representa las probabilidades de obtener todos los posibles resultados si el estudio se repitiera con nuevas muestras y la hipótesis nula fuera verdadera en la población.
- El modelo alternativo representa las probabilidades de obtener los resultados si el estudio se repitiera con nuevas muestras y la hipótesis alternativa fuera verdadera.
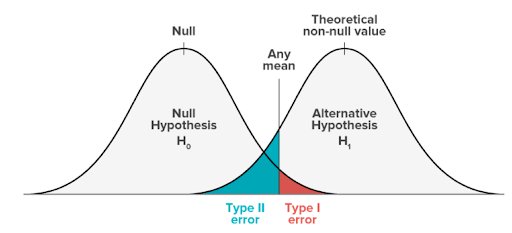
La zona sombreada representa la región crítica. Si tus resultados caen en la región crítica (área roja) de esta curva, se consideran estadísticamente significativos y se rechaza la hipótesis nula. No obstante, en estos casos esta sería una conclusión errónea (falso positivo), ya que la hipótesis nula en realidad es cierta.
El compromiso entre los errores tipo I y tipo II
En estadística, las tasas de error tipo I y error tipo II están relacionadas y se influyen mutuamente. El error tipo I depende del nivel de significancia, que a su vez afecta a la potencia estadística del test. Y la potencia estadística es inversamente proporcional a la tasa de error tipo II.
Esto significa que existe un compromiso entre los errores tipo I y tipo II:
- Un nivel de significancia bajo reduce el riesgo de error tipo I, pero aumenta el riesgo de error tipo II.
- Un test con alta potencia estadística puede tener un menor riesgo de error tipo II, pero mayor riesgo de error tipo I.
Ambos errores ocurren en la zona de solapamiento de las distribuciones de las dos hipótesis. El área roja representa alfa (tasa de error tipo I) y el área azul representa beta (tasa de error tipo II).
Por tanto, al fijar el nivel de error tipo I, también influimos indirectamente en el tamaño del error tipo II.
¿Cómo controlar los errores tipo I?
La probabilidad de cometer este error está vinculada al nivel de significancia (alfa o α) que definas.
Este valor, establecido al inicio del estudio, evalúa la probabilidad estadística de obtener los resultados (p-valor). El p-valor es un concepto ampliamente utilizado en la estadística frecuentista.
Según la literatura académica, el nivel de significancia suele fijarse en 0,05 o 5 %. Esto implica que, de 100 tests en los que las variaciones son idénticas, en 5 se concluirá erróneamente que son estadísticamente diferentes. Si el p-valor obtenido es inferior al nivel de significancia, la diferencia se considera estadísticamente significativa y consistente con la hipótesis alternativa. Si el p-valor es superior, la diferencia se considera estadísticamente no significativa.
Para reducir la probabilidad de error tipo I, puedes establecer un nivel de significancia menor y ejecutar los experimentos durante más tiempo para recoger más datos.
En VWO, utilizamos métricas como Probability to be the Best (PBB) y Absolute Potential Loss (PL) para determinar la variación ganadora. El uso conjunto de PBB y PL permite que, incluso si ocurre un error tipo I, el impacto de la decisión errónea sea asumible para el negocio.
Si quieres saber más sobre cómo VWO puede ayudarte a minimizar este tipo de errores, prueba gratis VWO o solicita una demo con uno de nuestros expertos en optimización.