Was ist ein Type 2 Error?
Nehmen wir an, ein Unternehmen möchte die Zahl der User des von ihm eingeführten Produkts erhöhen.
Das Unternehmen stellt die Hypothese auf, dass das Angebot einer kostenlosen Testversion die User dazu ermutigen könnte, das Produkt auszuprobieren und es für ihre Bedürfnisse zu bewerten. Um diese Hypothese zu überprüfen, führt das Unternehmen A/B-Tests mit den beiden Strategien durch – kostenlose Testversion und keine Testversion für die User. Nachdem das Experiment eine gewisse Zeit lang gelaufen ist, kommt der Test zu einem nicht-signifikanten Ergebnis. Da der Test keine eindeutigen Beweise für die vorgeschlagenen Hypothesen liefert, wird er abgelehnt und das Unternehmen beschließt, das kostenlose Testangebot einzustellen.
Nehmen wir nun an, dass die Testergebnisse in Wirklichkeit falsch waren und das Angebot kostenloser Testversionen die Zahl der User des Produkts tatsächlich erhöht hat. Dann hat der Test einen Falsch-Negativ- oder Type 2 Error verursacht. Wenn ein A/B-Test oder ein multivariater Test ein statistisch nicht signifikantes Ergebnis liefert, obwohl in Wirklichkeit ein Unterschied in der Leistung der getesteten Varianten besteht, handelt es sich um einen Type 2 Error.
Wissenschaftlich ausgedrückt, handelt es sich um einen Type 1 Error oder ein falsches Negativ, wenn ein Test die Nullhypothese (die keinen Effekt darstellt) nicht zurückweist, obwohl sie falsch ist und durch den Test zurückgewiesen werden sollte. Vor Beginn eines A/B-Tests oder MVT wird eine Nullhypothese definiert, die besagt, dass es keinen Unterschied zwischen den getesteten Varianten gibt.
Warum ist es wichtig, Type 2 Error zu verstehen?
Jeder Type 2 Error kann eine verpasste Chance zur Innovation sein und langfristig die Anzahl der Conversions erhöhen. Eine hohe Anzahl von Type 2 Errors kann dazu führen, dass viele potenziell gute Ideen verpasst werden, die zu einem Geschäftswachstum hätten führen können.
Ursachen für Type 2 Errors
Type 2 Errors stehen in umgekehrter Beziehung zur statistischen Aussagekraft eines Tests. Eine hohe statistische Aussagekraft hat einen geringen Type 2 Error zur Folge. Die statistische Aussagekraft ist die Wahrscheinlichkeit, mit der ein Hypothesentest einen statistischen Unterschied in der Conversion Rate zwischen den Varianten findet, wenn es einen Effekt gibt, der gefunden werden kann.
Die statistische Aussagekraft und der Mindestunterschied, um den Sie sich kümmern, bestimmen zusammen die Stichprobengröße eines Tests. Eine höhere statistische Aussagekraft und eine geringere Effektgröße können zu einer höheren Stichprobengröße führen, was eine höhere Testdauer bedeutet.
Ein Test ist nicht aussagekräftig genug, wenn er zu früh abgebrochen wird, was zu einer hohen Anzahl von Type 2 Error führen kann. Das macht es schwierig, selbst bei großen Effekten echte positive Ergebnisse zu entdecken.
Bei A/B- oder MVT-Tests gibt es einen Kompromiss zwischen der statistischen Genauigkeit und der Dauer des Tests. Je nach der für Ihr Unternehmen strategisch geeigneten Conversion Rate-Differenz und der statistischen Aussagekraft können Sie die praktikable Stichprobengröße für den Test bestimmen.
Grafische Darstellung von Type 2 Error
Im Folgenden finden Sie die Darstellung eines Nullhypothesenmodells und eines Alternativhypothesenmodells.
- Das Nullmodell stellt die Wahrscheinlichkeiten dar, alle möglichen Ergebnisse zu erhalten, wenn die Studie mit neuen Stichproben wiederholt würde und die Nullhypothese in der Population wahr wäre.
- Das Alternativmodell stellt die Wahrscheinlichkeit dar, dass alle möglichen Ergebnisse erzielt werden, wenn die Studie mit neuen Stichproben wiederholt wird und die Alternativhypothese in der Population zutrifft.
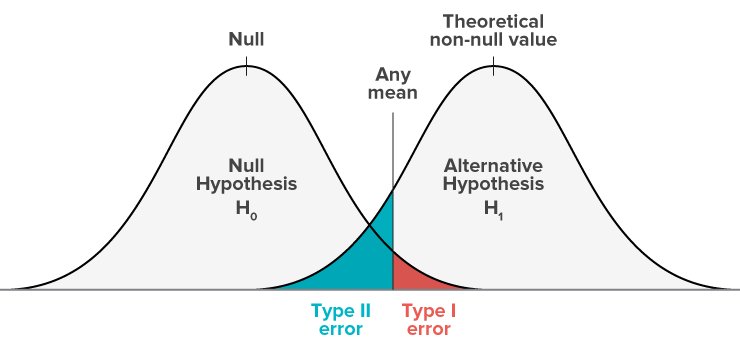
Der schattierte Bereich wird als kritischer Bereich bezeichnet. Wenn Ihre Ergebnisse in den blauen kritischen Bereich dieser Kurve fallen, werden sie als statistisch nicht signifikant angesehen und die Nullhypothese wird nicht verworfen. Dies ist jedoch eine falsche negative Schlussfolgerung, denn die Nullhypothese ist in diesen Fällen falsch und sollte abgelehnt werden.
Der Kompromiss zwischen Type 1 Error und Type 2 Error
Die Type 1 Error und Type 2 Error beeinflussen sich in der Statistik gegenseitig. Fehler vom Typ I hängen vom Signifikanzniveau ab, das die statistische Aussagekraft eines Tests beeinflusst. Die statistische Aussagekraft steht in umgekehrter Beziehung zur Fehlerquote vom Typ II.
Das bedeutet, dass es einen Kompromiss zwischen Type 1 und Type 2 Error gibt:
- Ein niedriges Signifikanzniveau verringert das Type 1 Error Risiko, erhöht aber das Type 2 Error Risiko.
- Ein kraftvoller Test kann ein geringeres Type 2 Error Risiko, aber ein hohes Type 1 Error Risiko haben.
Type 1 Error und Type 2 Error treten dort auf, wo sich die Verteilungen der beiden Hypothesen überschneiden. Der rot schattierte Bereich steht für Alpha, die Type 1 Error Quote, und der blau schattierte Bereich für Beta, die Type 2 Error Quote.
Indem Sie also die Type 2 Error Quote festlegen, beeinflussen Sie indirekt auch die Größe der Type 2 Error Quote.
Wie kontrolliert man den Type 2 Error?
Indem Sie die statistische Aussagekraft Ihres Tests erhöhen, können Sie das Risiko eines Type 2 Errors verringern. Die statistische Aussagekraft kann auf folgende Weise erhöht werden
- Erhöhen des Stichprobenumfangs
Mit zunehmender Stichprobengröße steigen die Chancen, einen Unterschied in einem Hypothesentest zu entdecken, was letztendlich zu einer erhöhten Aussagekraft eines Tests führt.
- Anhebung der Schwelle für das Signifikanzniveau
Die meisten statistischen Tests verwenden 0,05 als Schwellenwert für das Signifikanzniveau, um ein statistisch signifikantes Ergebnis zu ermitteln. Durch die Erhöhung des Signifikanzniveaus können Sie die Wahrscheinlichkeit erhöhen, dass die Nullhypothese abgelehnt wird, wenn sie wahr ist.
Indem Sie die Wahrscheinlichkeit der Ablehnung der Nullhypothese erhöhen, können Sie Type 2 Error verringern, aber auch die Wahrscheinlichkeit von Type 1 Error erhöhen. Daher müssen Sie die Auswirkungen von Type 1 und Type 2 Error bewerten und dementsprechend ein geeignetes Signifikanzniveau festlegen.
Bei VWO verwenden wir die Wahrscheinlichkeit, der Beste zu sein (Probability to be the Best – PBB) und den absoluten potenziellen Verlust (Absolute Potential Loss – PL) als Entscheidungsmetrik, um eine gewinnbringende Variante zu bestimmen. Die PBB-Metrik erfasst den Vorsprung, den eine Variante gegenüber den anderen konkurrierenden Varianten hat. Die Beibehaltung eines höheren PBB-Schwellenwerts kann die Anzahl der Type 2 Error reduzieren.
Wenn Sie mehr darüber erfahren möchten, wie genau VWO Ihnen helfen kann, solche Fehler zu reduzieren, probieren Sie die kostenlose VWO-Testversion aus oder fordern Sie eine Demo durch einen unserer Optimierungsexperten an.