Was ist ein Type 1 Error?
Stellen Sie sich eine Situation vor, in der ein E-Commerce-Unternehmen seine bestehenden Verkäufe verbessern möchte. Sie stellen die Hypothese auf, dass sie durch die Optimierung des Designs der Produktseite die Kaufrate verbessern können, was schließlich zu mehr Käufen führen würde.
Um diese Hypothese zu überprüfen, haben Sie A/B-Tests mit den beiden Designs durchgeführt und die Klickrate auf den Button für die Kaufabwicklung gemessen. Gemäß dem Hypothesentest-Ansatz eines A/B-Tests wird die neue Hypothese als wahr angesehen, wenn das Experiment eine bestimmte Zeit lang läuft und ein statistisch signifikantes Ergebnis zugunsten des neuen Produktseitendesigns erzielt wird.
Nehmen wir nun an, die Testergebnisse waren falsch und es gab tatsächlich keinen Unterschied zwischen den beiden Designs, dann hat der Test einen falsch positiven oder Type 1 Error begangen. Wenn ein A/B-Test oder ein multivariater Test ein statistisch signifikantes Ergebnis liefert, obwohl in Wirklichkeit kein Unterschied in der Leistung der getesteten Varianten besteht, handelt es sich um einen Type 1 Error.
Wissenschaftlich ausgedrückt, handelt es sich um einen Type 1 Error. Art oder einen Falsch-Positiv-Fehler, wenn während des Hypothesentests eine Nullhypothese (die keine Wirkung darstellt) abgelehnt wird, obwohl sie korrekt ist und durch den Test nicht abgelehnt werden sollte. Vor Beginn eines A/B-Tests oder MVT wird eine Nullhypothese definiert, die keinen Unterschied zwischen den getesteten Varianten darstellt.
Um es formaler auszudrücken: Wenn bei einem A/B-Test beide Varianten ähnlich sind und sich nicht unterschiedlich auf die getestete Metrik auswirken, kann ein Fehler auftreten, bei dem die Nullhypothese nach Abschluss des Tests zurückgewiesen wird. Wenn in einem solchen Fall festgestellt wird, dass es einen statistischen Unterschied zwischen den Varianten gibt, handelt es sich um einen Type 1 Error.
Warum ist es wichtig, Type 1 Error zu verstehen?
Nehmen wir an, Sie kommen nach der Durchführung eines A/B-Tests fälschlicherweise zu dem Schluss, dass Variante B der Gewinner ist, und setzen sie für den gesamten Daten-Traffic ein. Eine falsche Schlussfolgerung kann sich nachteilig auf die Conversion Rate eines Unternehmens auswirken und zu Umsatzeinbußen führen. Wenn Sie also einen A/B-Test durchführen, kann Ihnen das Verständnis der Type 1 Error helfen
- das Risiko abzuschätzen, falls eine falsche Schlussfolgerung gezogen wird
- Experimente durchzuführen, auf wissenschaftlich disziplinierte Weise
Was verursacht einen Type 1 Error?
Bei der Durchführung eines statistischen Tests besteht immer die Möglichkeit eines Type 1 Errors, da die Schätzungen auf der Grundlage einer begrenzten Stichprobe vorgenommen werden. Ein statistischer Test verspricht nicht, jedes Mal die richtigen Entscheidungen zu treffen, aber in den meisten Fällen die richtigen Entscheidungen. Daher muss eine Testmethodik danach beurteilt werden, wie gut sie in der Lage ist, die Fehler innerhalb einer bestimmten Grenze zu begrenzen.
Type 1 Error werden hauptsächlich aus zwei Gründen verursacht.
- Zufall – Bei einem Hypothesentest verwendet ein Analyst nur einen kleinen Teil der Grundgesamtheit der Daten, um Schätzungen vorzunehmen. Daher besteht die Möglichkeit, dass die gesammelten Stichproben in bestimmten Fällen nicht die wahre Population repräsentieren, was zu falschen Schlussfolgerungen führt.
- Frühzeitiges Abschließen eines Tests – Beim frequentistischen Hypothesentest wird erwartet, dass der Test durchgeführt wird, nachdem die für die Studie benötigte Stichprobengröße gesammelt wurde. Häufig werden die Tests jedoch beendet, sobald der p-Wert unter den festgelegten Schwellenwert fällt. Dies führt zu einer überhöhten falsch-positiven Rate.
Grafische Darstellung der Rate eines Type 1 Error
Im Folgenden finden Sie die Darstellung eines Nullhypothesenmodells und eines alternativen Hypothesenmodells.
- Das Nullmodell stellt die Wahrscheinlichkeit dar, alle möglichen Ergebnisse zu erhalten, wenn die Studie mit neuen Stichproben wiederholt würde und die Nullhypothese in der Population wahr wäre.
- Das Alternativmodell stellt die Wahrscheinlichkeit dar, alle möglichen Ergebnisse zu erhalten, wenn die Studie mit neuen Stichproben wiederholt wird und die Alternativhypothese in der Population wahr wäre.
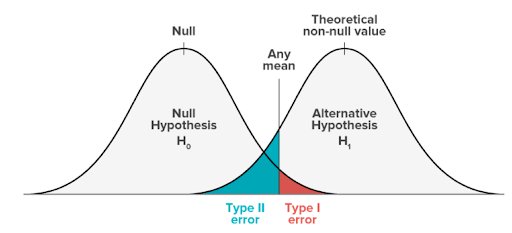
Der schattierte Bereich wird als kritischer Bereich bezeichnet. Wenn Ihre Ergebnisse in den roten kritischen Bereich dieser Kurve fallen, werden sie als statistisch signifikant angesehen und die Nullhypothese wird verworfen. Dies ist jedoch eine falsch positive Schlussfolgerung, denn die Nullhypothese ist in diesen Fällen tatsächlich wahr.
Der Kompromiss zwischen Type 1 und Type 2
Die Fehlerquoten vom Typ I und vom Typ II beeinflussen sich in der Statistik gegenseitig. Type 1 Error hängen vom Signifikanzniveau ab, das die statistische Aussagekraft eines Tests beeinflusst. Und die statistische Aussagekraft steht in umgekehrter Beziehung zur Fehlerrate vom Type 2 Error.
Das bedeutet, dass es einen Kompromiss zwischen den Type 1 Error und Type 2 Error gibt:
- Ein niedriges Signifikanzniveau verringert das Type 1 Error Risiko, erhöht aber das Type 2 Error Risiko.
- Ein kraftvoller Test kann ein geringeres Type 2 Error Risiko aufweisen, jedoch ein hohes Risiko Type 1 Errors.
Type 1 Error und Type 2 Error treten dort auf, wo sich die Verteilungen der beiden Hypothesen überschneiden. Der rot schattierte Bereich steht für Alpha, die Fehlerquote Typ I, und der blau schattierte Bereich für Beta, die Fehlerquote Typ II.
Indem Sie die Fehlerrate Typ I festlegen, beeinflussen Sie also indirekt auch die Größe der Fehlerrate Typ II.
Wie kann man die Type 1 Error kontrollieren?
Die Wahrscheinlichkeit, diesen Fehler zu begehen, hängt mit dem Signifikanzniveau (Alpha oder α) zusammen, das Sie festlegen.
Dieser Wert, den Sie zu Beginn Ihrer Studie festlegen, bewertet die statistische Wahrscheinlichkeit, Ihre Ergebnisse zu erhalten (p-Wert). Der p-Wert ist ein Begriff, der hauptsächlich in der frequentistischen Statistik verwendet wird.
In der akademischen Literatur wird das Signifikanzniveau normalerweise auf 0,05 oder 5% festgelegt. Das bedeutet, dass von 100 Tests, bei denen die Variationen gleich sind, 5 Tests besagen, dass die Variationen statistisch unterschiedlich sind. Wenn der erhaltene p-Wert Ihres Tests niedriger ist als das konfigurierte Signifikanzniveau, bedeutet dies, dass der Unterschied statistisch signifikant ist und mit der alternativen Hypothese übereinstimmt.Der Unterschied ist jedoch statistisch nicht signifikant, wenn der p-Wert höher als das Signifikanzniveau ist.
Um die Wahrscheinlichkeit eines Type 1 Error zu verringern, können Sie einfach ein niedrigeres Signifikanzniveau einstellen und die Experimente länger laufen lassen, um mehr Daten zu sammeln.
Bei VWO verwenden wir die Wahrscheinlichkeit, der Beste zu sein (Probability to be the Best, PBB) und den absoluten potenziellen Verlust (Absolute Potential Loss, PL) als Entscheidungsmetrik, um eine Gewinnvariante zu bestimmen. Die Verwendung der PL-Metrik mit PBB stellt sicher, dass selbst bei einem Type 1 Error die Gesamtauswirkungen der falschen Entscheidung für das Unternehmen tolerierbar sind.
Um mehr darüber zu erfahren, wie genau VWO Ihnen helfen kann, solche Fehler zu reduzieren, testen Sie die kostenlose VWO-Testversion oder fordern Sie eine Demo durch einen unserer Optimierungsexperten an.