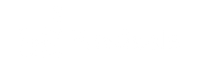Wie berechnet man die Stichprobengrößen für A/B-Tests?

(Dieser Beitrag ist eine wissenschaftliche Erklärung der optimalen Stichprobengröße für Ihre Tests, damit diese statistisch korrekt sind. Die Testberichterstattung von VWO ist so konzipiert, dass Sie Ihre Zeit nicht mit der Suche nach p-Werten oder der Bestimmung der statistischen Signifikanz verschwenden – die Plattform meldet die „Gewinnwahrscheinlichkeit“ und macht die Testergebnisse leicht interpretierbar. Melden Sie sich für eine kostenlose Testversion hier an.)

„Wie groß muss die Sample Size sein?“

In der Online-Welt sind die Möglichkeiten für A/B-Testings so gut wie unbegrenzt. Und in der Tat werden viele Experimente durchgeführt, deren Ergebnisse nach den Regeln des Null-Hypothesen-Tests interpretiert werden: Sind diese Ergebnisse statistisch signifikant?

Ein wichtiger Aspekt bei der Arbeit der Datenbankanalysten ist deshalb die Festlegung geeigneter Stichprobengrößen für diese Tests.

Kostenlos herunterladen: A/B-Testing Leitfaden

Anhand eines Alltagsfalles besprechen wir einige aktuelle Ansätze zur Berechnung der erforderlichen Stichprobengröße.

Der Fall zur Berechnung der Stichprobengröße:

Ein Marketer hat sich eine Alternative für eine Landing Page ausgedacht und möchte diese Alternative testen. Die ursprüngliche Landing Page hat eine bekannte Conversion von 4%. Die erwartete Conversion der alternativen Seite beträgt 5%. Der Marketer fragt also den Analysten: „Wie groß sollte die Stichprobe sein, um mit statistischer Signifikanz nachzuweisen, dass die Alternative besser ist als das Original?“

Lösung: „Standard-Stichprobenumfang“

Der Analyst gibt aus Gewohnheit an: Split-Run (A/B-Test) mit jeweils 5.000 Beobachtungen und einem einseitigen Test mit einer Reliabilität von .95.

Was geschieht hier?

Was passiert, wenn man zwei Stichproben zieht, um den Unterschied zwischen den beiden zu schätzen, wobei ein einseitiger Test mit einer Reliabilität von .95 durchgeführt wird? Sie können dies veranschaulichen, indem Sie unendlich viele Stichproben mit jeweils 5.000 Beobachtungen aus einer Population mit einer Conversion von 4% ziehen und den Unterschied in der Conversion pro Paar (pro ‚Test‘) zwischen den beiden Stichproben in einem Diagramm darstellen.

Abbildung 1: Stichprobenverteilung für die Differenz zwischen zwei Proportionen mit p1=p2=.04 und n1=n2=5.000; ein Signifikanzbereich ist für alpha=.05 (Reliabilität= .95) bei einem einseitigen Test angegeben.

Dieses Diagramm spiegelt das wider, was formal als „Stichprobenverteilung für die Differenz zwischen zwei Proportionen“ bezeichnet wird. Es ist die Wahrscheinlichkeitsverteilung aller möglichen Stichprobenergebnisse, die für die Differenz zwischen p1=p2=.04 und n1=n2=5.000 berechnet wurden. Diese Verteilung ist die Grundlage – die Referenzverteilung – für den Nullhypothesentest. Die Nullhypothese lautet, dass es keinen Unterschied zwischen den beiden Landing Pages gibt. Dies ist die Verteilung, die für die eigentliche Entscheidung über Signifikanz oder Nicht-Signifikanz verwendet wird.

p=.04 bedeutet 4% Conversion. Statistiker sprechen in der Regel von Proportionen, die zwischen 0 und 1 liegen können, während in der Alltagssprache meist von Prozentsätzen die Rede ist. Um der Tabelle gerecht zu werden, wird die Proportionsschreibweise verwendet.

Diese Wahrscheinlichkeitsverteilung lässt sich grob mit dieser spss-Syntax nachbilden (thirty paired samples from a population.sps). Nicht unendlich, aber 30 Mal werden zwei Stichproben mit p1=p2=.04 und n1=n2=5.000 gezogen. Die Differenz zwischen den beiden Stichproben wird dann in einem Histogramm mit der eingegebenen Normalverteilung dargestellt (das letzte Diagramm im Output). Diese Normalkurve wird der Kurve in Abbildung 1 recht ähnlich sein. Der Grund für die Durchführung dieses Experiments ist die Demonstration des Wesens einer Stichprobenverteilung.

Der Modalwert des Unterschieds in der Umwandlung zwischen den beiden Gruppen ist Null. Das macht Sinn, denn beide Gruppen stammen aus der gleichen Population mit einem Umsatz von 4%. Abweichungen von Null sowohl nach links (Original schneidet besser ab) als auch nach rechts (Alternative schneidet besser ab) können und werden zufällig auftreten. Je weiter sie jedoch von Null abweichen, desto geringer ist die Wahrscheinlichkeit, dass sie auftreten. Der rosa Bereich mit dem Zeichen Alpha ist der Signifikanzbereich oder Unzuverlässigkeit=1-Zuverlässigkeit=1-.95.

Wenn bei einem Test der Unterschied in der Conversion zwischen der alternativen Seite und der Originalseite in den rosafarbenen Bereich fällt, dann wird die Nullhypothese – dass es keinen Unterschied zwischen den beiden Seiten gibt – zugunsten der Hypothese verworfen, dass die alternative Seite eine höhere Conversion als die Originalseite liefert. Die Logik dahinter ist, dass ein solches Ergebnis ein eher „seltenes“ Ergebnis wäre, falls die Nullhypothese tatsächlich wahr wäre.

Die x-Achse in Abbildung 1 zeigt nicht den Wert der Teststatistik (in diesem Fall Z), wie es normalerweise der Fall wäre. Der Übersichtlichkeit halber wurde der konkrete Unterschied in der Conversion zwischen den beiden Landing Pages dargestellt.

Wenn also in einem Split-Run-Test die alternative Landing Page eine um 0,645% höhere oder höhere Conversion Rate als die ursprüngliche Landing Page liefert (und damit in den Signifikanzbereich fällt), dann wird die Nullhypothese, die besagt, dass es keinen Unterschied in der Conversion zwischen den Landing Pages gibt, zugunsten der Hypothese verworfen, dass die Alternative besser abschneidet (die 0,645% entsprechen einem statistischen Z-Wert von 1,65).

Der Vorteil des Ansatzes „Standard-Stichprobenumfang“ ist, dass durch die Wahl eines festen Stichprobenumfangs eine gewisse Standardisierung eingebracht wird. Verschiedene Tests sind vergleichbar und haben in dieser Hinsicht „die gleiche Chance“.

Der Nachteil dieses Ansatzes ist, dass die Wahrscheinlichkeit, die Nullhypothese abzulehnen, wenn die Nullhypothese (H₀ ) wahr ist, bekannt ist, nämlich das selbst gewählte Alpha von.05, während die Wahrscheinlichkeit, H₀ nicht abzulehnen, wenn H₀ nicht wahr ist, unbekannt bleibt. Es handelt sich um zwei Fehlentscheidungen, die als Fehler Typ 1 bzw. Typ 2 bezeichnet werden.

Ein Fehler vom Typ 1 oder Alpha liegt vor, wenn H₀  abgelehnt wird, obwohl H₀ tatsächlich wahr ist. Alpha ist die Wahrscheinlichkeit, dass das Ergebnis eines Tests einen Effekt für die Manipulation aufweist, während auf Populationsebene tatsächlich kein Effekt vorhanden ist. 1-Alpha ist die Wahrscheinlichkeit, die Nullhypothese zu akzeptieren, wenn sie wahr ist – eine korrekte Entscheidung –. Dies wird als Reliabilität bezeichnet.

Ein Fehler Typ 2, oder Beta, wird gemacht, wenn H₀  nicht verworfen wird, obwohl H₀ nicht wahr ist. Beta ist die Wahrscheinlichkeit zu sagen, dass das Ergebnis eines Tests keinen Effekt für die Manipulation hat, während er auf Populationsebene tatsächlich vorhanden ist. 1-Beta ist die Chance, die Nullhypothese abzulehnen, wenn sie nicht wahr ist – eine korrekte Entscheidung –. Dies wird als Power bezeichnet.

Die Aussagekraft ist eine Funktion von Alpha, Stichprobengröße und Effekt (der Effekt ist hier der Unterschied in der Conversion zwischen den beiden Landing Pages, d. h. auf Populationsebene der Mehrwert der alternativen Seite im Vergleich zur ursprünglichen Seite). Je kleiner Alpha, Stichprobengröße oder Effekt, desto geringer ist die Aussagekraft.

In diesem Beispiel wird Alpha vom Analysten auf 0,05 gesetzt. Die Stichprobengröße wird ebenfalls vom Analysten festgelegt: 5000 für die ursprüngliche und 5000 für die alternative Stichprobe. Bleibt noch der Effekt. Und der tatsächliche Effekt ist per Definition unbekannt. Es ist jedoch nicht unrealistisch, kommerzielle Ziele oder Erfahrungswerte als Ankerwert zu verwenden, wie es im vorliegenden Fall vom Marketer formuliert wurde: eine erwartete Verbesserung von 4% auf 5%. Wäre dieser Effekt tatsächlich eingetreten, würde der Marketer natürlich statistisch signifikante Ergebnisse in einem Test finden wollen.

Ein Beispiel mag helfen, dieses Konzept deutlich zu machen und die Bedeutung der Potenz zu verdeutlichen: Nehmen wir an, die tatsächliche (=Populations-) Conversion der alternativen Seite beträgt tatsächlich 5%. Die Stichprobenverteilung für die Differenz zwischen zwei Anteilen mit Conversion1=4%, Conversion2=5% und n1=n2=5.000 wird in Kombination mit der zuvor gezeigten Stichprobenverteilung für die Differenz zwischen zwei Anteilen mit Conversion1=Conversion2=4% und n1=n2=5.000 aufgetragen (Abbildung 1).

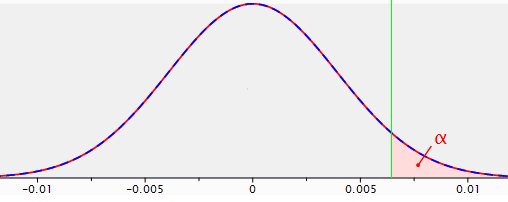
Abbildung 2: Stichprobenverteilungen für die Differenz zwischen zwei Proportionen mit p1=p2=.04, n1=n2=5.000 (rote Linie) und p1=.04, p2=.05, n1=n2=5.000 (gestrichelte blaue Linie), mit einem einseitigen Test und einer Reliabilität von .95.

Die gestrichelte blaue Linie zeigt die Stichprobenverteilung der Differenz der Conversion Rates zwischen Original und Alternative, wenn in Wirklichkeit (auf Populationsebene) die Originalseite 4% und die alternative Seite 5% Conversion erzielt, bei Stichproben von jeweils 5.000. Die Stichprobenverteilung für den Fall, dass H₀ wahr ist – die rote Linie – hat sich grundsätzlich nach rechts verschoben. Der Modalwert dieser neuen Verteilung mit dem angenommenen Effekt von 1% ist natürlich 1%, mit zufälligen Abweichungen sowohl nach links als auch nach rechts.

Nun werden alle Ergebnisse, d. h. Testergebnisse, auf der rechten Seite der grünen Linie (die den Signifikanzbereich markiert) als signifikant angesehen. Alle Beobachtungen auf der linken Seite der grünen Linie gelten als nicht signifikant. Der Bereich unter der „blauen“ Verteilung links von der Signifikanzlinie ist Beta, die Chance, H₀ nicht zurückzuweisen, wenn H₀ tatsächlich nicht wahr ist (eine falsche Entscheidung), und er umfasst 22% dieser Verteilung.

Damit ist die Fläche unter der blauen Verteilung rechts von der Signifikanzlinie die Potenzfläche, und diese Fläche deckt 78% der Stichprobenverteilung ab. Die Wahrscheinlichkeit, H₀ zu verwerfen, wenn H₀ nicht wahr ist, ist eine richtige Entscheidung.

Die Aussagekraft dieses spezifischen Tests mit seinen spezifischen Parametern beträgt also .78.

In 78% der Fälle, in denen dieser Test durchgeführt wird, ergibt sich ein signifikanter Effekt und folglich eine Ablehnung von H₀. Das könnte akzeptabel sein, oder vielleicht auch nicht; das ist eine Frage, über die sich Marketer und Analysten einigen müssen.

Keine einfache Sache, aber wichtig. Nehmen wir zum Beispiel an, dass die Erwartung einer 10%igen Steigerung des Umsatzes sowohl realistisch als auch kommerziell interessant wäre: 4,0% beim Original gegenüber 4,4% bei der Alternative. Dann ändert sich die Situation wie folgt.

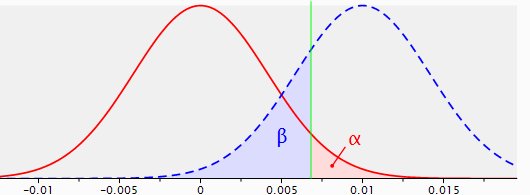
Abbildung 3: Stichprobenverteilungen für die Differenz zwischen zwei Anteilen mit p1=p2=.040, n1=n2=5.000 (rote Linie) und p1=.040, p2=.044, n1=n2=5.000 (gestrichelte blaue Linie), mit einem einseitigen Test und einer Reliabilität von .95.

Unter diesen Umständen wäre der Test nicht sehr sinnvoll, sondern sogar kontraproduktiv, da die Wahrscheinlichkeit, dass ein solcher Test zu einem signifikanten Ergebnis führt, nur 0,26 beträgt.

Die oben genannten Zahlen wurden mit der Anwendung „Gpower“ berechnet und erstellt:

Dieses Programm berechnet die erreichte Performance für viele Arten von Tests, basierend auf der gewünschten Stichprobengröße, Alpha und dem vermuteten Effekt.

Ebenso kann der erforderliche Stichprobenumfang aus der gewünschten Performance, Alpha und dem erwarteten Effekt berechnet werden, das erforderliche Alpha kann aus der gewünschten Performance, dem Stichprobenumfang und dem erwarteten Effekt berechnet werden und der erforderliche Effekt kann aus der gewünschten Performance, Alpha und dem Stichprobenumfang berechnet werden.

Sollte eine Trennschärfe von 0,95 bei einem angenommenen p1=.040, p2=.044 angestrebt werden, so beträgt der erforderliche Stichprobenumfang jeweils 54.428.

Abbildung 4: Stichprobenverteilungen für die Differenz zwischen zwei Anteilen mit p1=p2=.040 (rote Linie) und p1=.040, p2=.044 (gestrichelte blaue Linie), unter Verwendung eines einseitigen Tests, mit einer Reliabilität von .95 und einer Potenz von .95.

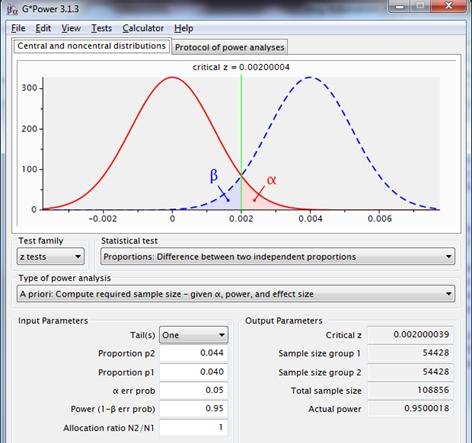
Diese Abbildung zeigt Informationen, die in den vorherigen Diagrammen fehlen. Sie vermittelt auch einen Eindruck von der Schnittstelle des Programms.

Kostenlos herunterladen: A/B-Testing Leitfaden

Wichtige Aspekte der Power-Analyse sind die sorgfältige Bewertung der Folgen der Ablehnung der Nullhypothese, wenn die Nullhypothese tatsächlich zutrifft – z. B. wird auf der Grundlage der Testergebnisse eine kostspielige Kampagne unter der Annahme durchgeführt, dass sie ein Erfolg sein wird, und dieser Erfolg stellt sich nicht ein -, und die Folgen der Nichtablehnung der Nullhypothese, wenn die Nullhypothese nicht zutrifft – z. B. wird auf der Grundlage der Testergebnisse eine Kampagne nicht durchgeführt, obwohl sie ein Erfolg gewesen wäre.

Lösung: „Standardanzahl der Conversions“

Der Analyst gibt an: Split-Run mit mindestens 100 Conversions pro konkurrierender Seite und ein einseitiger Test mit einer Reliabilität von .95.

Im aktuellen Fall mit einer erwarteten Conversion der Originalseite von 4% und einer erwarteten Conversion der Alternativseite von 5% wird ein Minimum von 2.500 Beobachtungen pro Seite empfohlen.

Bei der Prüfung der Potenz zeigt dieses Szenario jedoch eine Potenz von nur wenig mehr als 0,5.

Abbildung 5: Stichprobenverteilungen für die Differenz zwischen zwei Proportionen mit p1=p2=.04, n1=n2=2500 (rote Linie) und p1=.04, p2=.05, n1=n2=2500 (gestrichelte blaue Linie) unter Verwendung eines einseitigen Tests mit einer Reliabilität von .95.

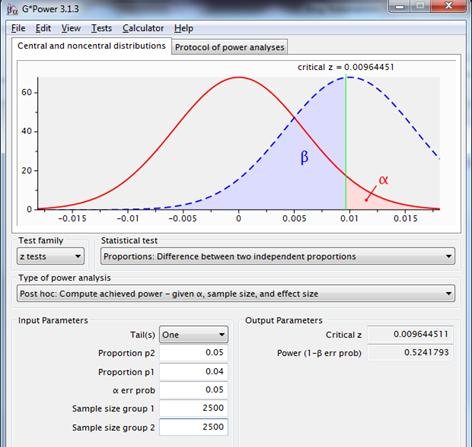
Für eine bessere Aussagekraft sollte ein größerer Effekt vorhanden sein, eine größere Stichprobe gewählt oder Alpha erhöht werden, z. B. auf 0,2:

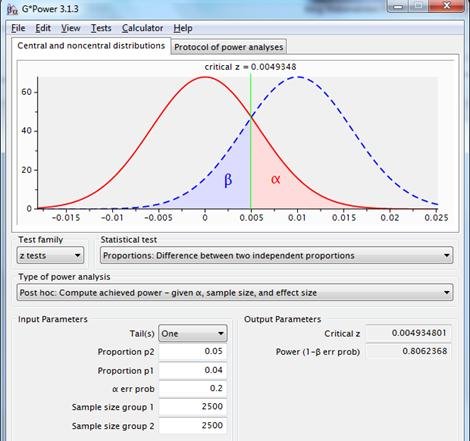
Ein Alpha von 0,2 ergibt eine Potenz von 0,8. Die Aussagekraft ist akzeptabler; der „Preis“ für diese höhere Aussagekraft besteht in einer größeren Chance, H₀ abzulehnen, wenn H₀ tatsächlich wahr ist.

Auch hier spielen geschäftliche Erwägungen, die die Auswirkungen von Alpha und Beta betreffen, eine wichtige Rolle bei solchen Entscheidungen.

Der Ansatz „Standardanzahl von Conversions“ mit seiner Faustregel für die Anzahl der Conversions setzt tatsächlich eine Art Grenze für Effektgrößen, die noch sinnvoll getestet werden können (d. h. mit einer angemessenen Aussagekraft). In dieser Hinsicht beinhaltet er auch eine Art Standardisierung, und das ist an sich kein Problem, solange seine Konsequenzen verstanden und anerkannt werden.

Lösung: „Signifikantes Probenergebnis“

Der Analytiker gibt an: Split Run mit genügend Beobachtungen, um ein statistisch signifikantes Ergebnis zu erhalten, wenn im Test der vermutete Effekt tatsächlich auftritt, einseitig getestet mit einer Reliabilität von .95.

Das klingt ein wenig seltsam, und das ist es auch. Leider wird diese Logik in der Praxis häufig angewandt. Die erforderliche Stichprobengröße wird grundsätzlich unter der Annahme berechnet, dass der vermutete Effekt in der Stichprobe tatsächlich auftritt.

Im verwendeten Beispiel: Wenn in einem Test das Original eine Umwandlung von 4% und die Alternative 5% hat, dann wären 2.800 Fälle pro Gruppe notwendig, um statistische Signifikanz zu erreichen. Dies lässt sich mit der zugehörigen spss-Syntax (limit at significant test result.sps) demonstrieren.

Diese Art von Berechnungen wird von verschiedenen Online-Tools angewendet, die die Berechnung der Stichprobengröße anbieten. Bei diesem Ansatz wird das Konzept des Zufallsstichprobenfehlers ignoriert und somit das Wesen der Inferenzstatistik und der Nullhypothesenprüfung außer Acht gelassen. In der Praxis ergibt dies immer eine Trennschärfe von 0,5 plus einen kleinen zusätzlichen Überschuss.

Abbildung 7: Stichprobenverteilungen für die Differenz zwischen zwei Anteilen mit p1=p2=.04, n1=n2=2800 (rote Linie) und p1=.04, p2=.05, n1=n2=2800 (gestrichelte blaue Linie), unter Verwendung eines einseitigen Tests, mit einer Reliabilität von .95.

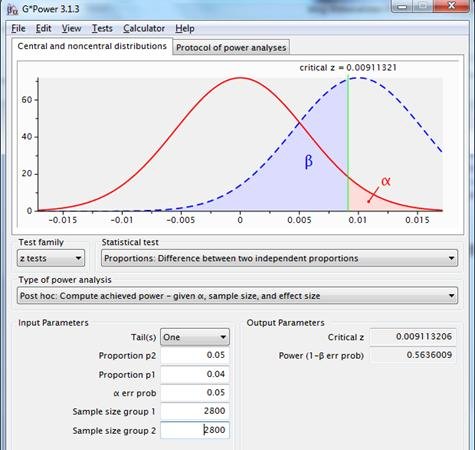
Mit diesem System wird zwar auch eine Art Standardisierung vorgenommen, nämlich bei der Performance, aber das ist nicht das offensichtliche Ziel, für das diese Methode erfunden wurde.

Lösung: „Standard-Reliabilität und Performance“

Der Analyst gibt an: Split Run mit einer Aussagekraft von .8 und einer Reliabilität von .95 bei einem einseitigen Test.

Im aktuellen Fall mit 4% Conversion für die Originalseite und 5% erwarteter Conversion für die alternative Seite, alpha=.05 und power=.80, empfiehlt Gpower zwei Stichproben von 5313.

Abbildung 8: Stichprobenverteilungen für die Differenz zwischen zwei Proportionen mit p1=p2=.04 (rote Linie) und p1=.04, p2=.05 (gestrichelte blaue Linie), unter Verwendung eines einseitigen Tests mit Reliabilität .95 und Power .80.

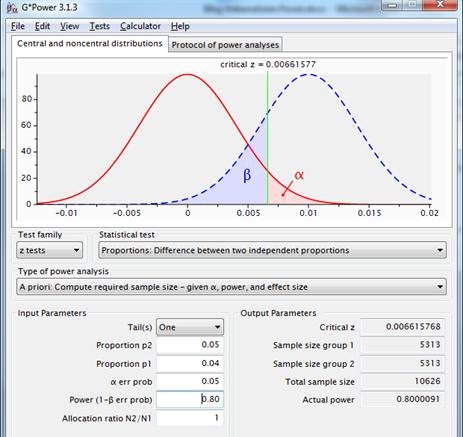
Bei diesem Ansatz werden die gewünschte Reliabilität, der erwartete Effekt und die gewünschte Aussagekraft für die Berechnung des erforderlichen Stichprobenumfangs herangezogen.

Jetzt hat der Analytiker die Wahrscheinlichkeit im Griff, mit der ein erwarteter/gewünschter/notwendiger Effekt zu statistisch signifikanten Ergebnissen in einem Test führt, nämlich .8.

Einige Online-Tools, z. B. der Rechner für die Dauer von Split Tests von VWO, verwenden bei der Berechnung der Stichprobengröße das Konzept der Power.

In einer Präsentation von VWO „Visitors needed for A/B testing“ wird eine Potenz von 0,8 als übliches Maß genannt.

Man kann sich fragen, warum das eine akzeptable Regel sein sollte? Warum kann die Größe der Performance und die Größe der Reliabilität nicht dynamischer genutzt werden?

Lösung: „Gewünschte Reliabilität und Performance“

Der Analyst gibt an: Splitlauf mit gewünschter Performance und Reliabilität in einem einseitigen Test.

Es folgt eine Diskussion darüber, was in diesem Fall akzeptable Performance und Zuverlässigkeit ist, mit der Schlussfolgerung, dass beide 90% betragen. Ergebnis laut Gpower, 2 mal 5.645 Beobachtungen:

Abbildung 9: Stichprobenverteilungen für die Differenz zwischen zwei Proportionen mit p1=p2=.04 (rote Linie) und p1=.04, p2=.05 (gestrichelte blaue Linie), unter Verwendung eines einseitigen Tests mit Reliabilität=.90 und Potenz=.90.

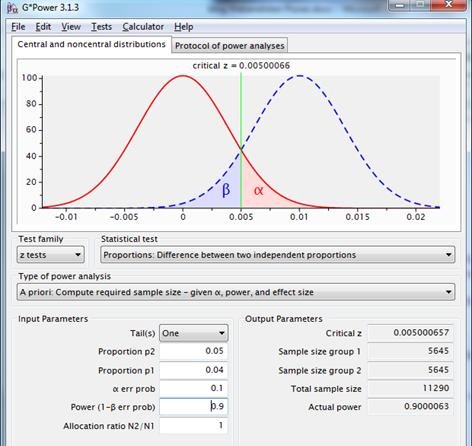
Was, wenn der Marketer sagt: „Es dauert zu lange, so viele Beobachtungen zu sammeln. Die Landing Page wird dann nicht mehr wichtig sein. Es ist Platz für insgesamt 3.000 Testbeobachtungen. Reliabilität ist genauso wichtig wie Performance. Der Test sollte möglichst durchgeführt werden und eine Entscheidung sollte folgen“?

Ergebnis auf der Grundlage dieser Einschränkung: Reliabilität und Aussagekraft liegen beide bei 0,75. Wenn dies für die Betroffenen keine Probleme aufwirft, kann der Test auf der Grundlage von Alpha=.25 und Power=.75 fortgesetzt werden.

Abbildung 10: Stichprobenverteilungen für die Differenz zwischen zwei Proportionen mit p1=p2=.04, n1=n2=1500 (rote Linie) und p1=.04, p2=.05, n1=n2=1500 (gestrichelte blaue Linie), unter Verwendung eines einseitigen Tests mit gleicher Reliabilität und Potenz.

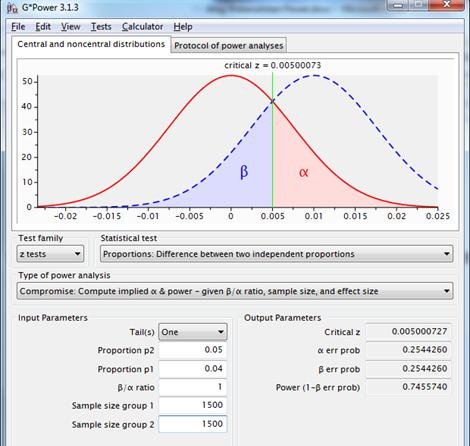
Dieser Ansatz ermöglicht eine flexible Wahl von Reliabilität und Performance. Nachteilig ist die fehlende Standardisierung

Schlussfolgerung

Es gibt mehrere Ansätze zur Berechnung des erforderlichen Stichprobenumfangs, die von fragwürdiger Logik bis hin zu sehr fundiert reichen.

Bei strategisch wichtigen „entscheidenden Experimenten“ wird die umfassendste Methode bevorzugt, bei der sowohl die „gewünschte Reliabilität als auch die Power“ in die Berechnung einbezogen werden. Wenn es keine Möglichkeit gibt, gegen frühere Effekte zu prüfen, kann ein Effekt mit Hilfe eines Pilotversuchs mit „Standard-Stichprobengröße“ oder „Standard-Anzahl von Conversions“ geschätzt werden.

Für die Mehrzahl der Entscheidungen im Laufe des Jahres wird aus Gründen der Vergleichbarkeit zwischen den Tests die „Standard-Reliabilität und -Performance“ empfohlen.

Die Arbeit mit den empfohlenen Ansätzen auf der Grundlage des kalkulierten Risikos führt zu einer wertvollen Optimierung und richtigen Entscheidungsfindung.

Hinweis: Die in diesem Blog verwendeten Screenshots sind Eigentum des Autors.

FAQs zum Stichprobenumfang bei A/B-Testings