(Este post es una explicación científica del tamaño óptimo de la muestra para que tus tests sean estadísticamente correctas. Los informes de los tests de VWO están diseñados para que no pierdas el tiempo buscando valores p o determinando la significación estadística: la plataforma informa de la «probabilidad de ganar» y hace que los resultados de las tests sean fáciles de interpretar. Regístrate para una prueba gratuita aquí)
‘¿Cómo de grande tiene que ser el tamaño de la muestra?‘
En el mundo online, las posibilidades de realizar tests A/B con casi cualquier cosa son inmensas. Y de hecho se hacen muchos experimentos, cuyo resultado se interpreta siguiendo las reglas de la prueba de hipótesis nula, «¿son los resultados estadísticamente significativos?».
Por tanto, un aspecto importante en el trabajo del analista de bases de datos es determinar los tamaños de muestra adecuados para estas pruebas.
Descargar gratis: Guía de tests A/B
A partir de un caso cotidiano, se discuten varios enfoques actuales para calcular el tamaño de muestra deseado.
Caso para calcular el tamaño de la muestra:
El vendedor ha ideado una alternativa para una landing page y quiere ponerla a prueba. La landing page original tiene una conversión conocida del 4%. La conversión esperada de la página alternativa es del 5%. Así que el comercializador pregunta al analista «¿qué tamaño debe tener la muestra para demostrar con significación estadística que la alternativa es mejor que la original?».
Solución: ‘tamaño de muestra por defecto’
El analista dice: ejecución dividida (test A/B) con 5.000 observaciones cada una y una prueba unilateral con una fiabilidad de 0,95. Por costumbre.
¿Qué ocurre aquí?
¿Qué ocurre al extraer dos muestras para estimar la diferencia entre ambas, con una prueba unilateral y una fiabilidad del 0,95? Esto puede demostrarse extrayendo infinitamente dos muestras de 5.000 observaciones cada una de una población con una conversión del 4%, y trazando la diferencia de conversión por par (por «prueba») entre las dos muestras en un gráfico.
Figura 1: distribución muestral para la diferencia entre dos proporciones con p1=p2=.04 y n1=n2=5.000; se indica un área de significación para alfa=.05 (fiabilidad= .95) utilizando una prueba unilateral.
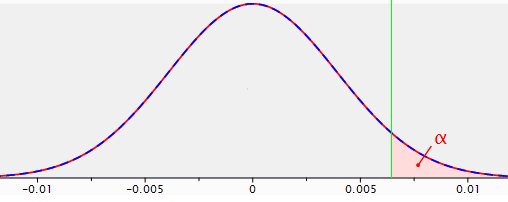
Este gráfico refleja lo que formalmente se denomina «distribución muestral para la diferencia entre dos proporciones». Es la distribución de probabilidad de todos los posibles resultados muestrales calculados para la diferencia entre p1=p2=.04 yn1=n2=5.000. Esta distribución es la base -la distribución de referencia- para la prueba de hipótesis nulas. La hipótesis nula es que no hay diferencia entre las dos landing page. Es la distribución que se utiliza para decidir realmente sobre la significación o no significación.
p=.04 significa una conversión del 4%. Los estadísticos suelen hablar de proporciones que pueden estar comprendidas entre 0 y 1, mientras que en el lenguaje cotidiano se comunican sobre todo porcentajes. Para ajustarse al gráfico, se utiliza la notación de proporción.
Esta distribución de probabilidad puede reproducirse aproximadamente utilizando esta sintaxis spss (treinta muestras pareadas de una población.sps). No infinitamente, pero 30 veces se extraen dos muestras con p1=p2=.04 y n1=n2=5.000. A continuación, la diferencia entre las dos muestras se representa en un histograma con la distribución normal introducida (el último gráfico de la salida). Esta curva normal será bastante similar a la curva de la figura 1. El motivo de realizar este experimento es demostrar la esencia de una distribución muestral.
El valor modal de la diferencia de conversión entre los dos grupos es cero. Eso tiene sentido, ambos grupos proceden de la misma población con una conversión del 4%. Las desviaciones de cero tanto a la izquierda (el original lo hace mejor) como a la derecha (el alternativo lo hace mejor) pueden ocurrir y ocurrirán, simplemente por azar. Sin embargo, cuanto más se alejen de cero, menor será la probabilidad de que ocurran. El área rosa con el carácter alfa indicado en ella es el área de significación, o no fiabilidad=1-fiabilidad=1-,95.
Si en una prueba la diferencia de conversión entre la página alternativa y la página original cae en la zona rosa, entonces se rechaza la hipótesis nula de que no hay diferencia entre ambas páginas a favor de la hipótesis de que la página alternativa devuelve una conversión mayor que la original. La lógica subyacente es que, si la hipótesis nula fuera realmente cierta, ese resultado sería bastante «raro».
El eje x de la figura 1 no muestra el valor de la estadística de prueba (Z en este caso), como sería habitual. En aras de la claridad, se ha mostrado la diferencia concreta de conversión entre las dos landing page.
Así, cuando en un split test la landing page alternativa arroja una tasa de conversión un 0,645% mayor o más que la landing page original (por tanto, entra en la zona de significación), entonces se rechaza la hipótesis nula que afirma que no hay diferencia de conversión entre las landing pages a favor de la hipótesis de que la alternativa lo hace mejor (el 0,645% corresponde a un valor Z de la estadística de prueba de 1,65).
La ventaja del enfoque «tamaño de muestra por defecto» es que, al elegir un tamaño de muestra fijo, se introduce una cierta normalización. Varias pruebas son comparables «tienen las mismas posibilidades» a ese respecto.
El inconveniente de este enfoque es que, mientras que la probabilidad de rechazar la hipótesis nula cuando la hipótesis nula (H0 ) es cierta es bien conocida, a saber, el alfa autoseleccionado de 0,05, la probabilidad de no rechazar H0 cuando H0 no es cierta sigue siendo desconocida. Se trata de dos decisiones falsas, conocidas como error de tipo 1 y error de tipo 2, respectivamente.
Se comete un error de tipo 1, o alfa, cuando se rechaza H0 , cuando en realidad es cierta H0 . Alfa es la probabilidad de decir en el resultado de una prueba que hay un efecto de la manipulación, cuando en realidad no lo hay a nivel poblacional. 1-alfa es la probabilidad de aceptar la hipótesis nula cuando es cierta -una decisión correcta-. Esto se llama fiabilidad.
Se comete un error de tipo 2, o beta, cuando no se rechaza H0 , cuando en realidad H0 no es cierta. Beta es la probabilidad de decir en el resultado de una prueba que no hay efecto de la manipulación, cuando en realidad sí lo hay a nivel poblacional. 1-beta es la probabilidad de rechazar la hipótesis nula cuando no es cierta -una decisión correcta-. Esto se llama potencia.
La potencia es una función de alfa, el tamaño de la muestra y el efecto (el efecto aquí es la diferencia de conversión entre las dos landing pages, es decir, a nivel de población, el valor añadido del sitio alternativo en comparación con el sitio original). Cuanto menores sean el alfa, el tamaño de la muestra o el efecto, menor será la potencia.
En este ejemplo, el analista fija el alfa en 0,05. El analista también fija el tamaño de las muestras: 5000 para la original y 5000 para la alternativa. Queda el efecto. Y el efecto real es, por definición, desconocido. Sin embargo, no deja de ser realista utilizar objetivos comerciales o cifras de experiencia como valor de anclaje, como formuló el comercializador en el caso actual: una mejora esperada del 4% al 5%. Ahora bien, si ese efecto fuera realmente cierto, el comercializador querría, por supuesto, encontrar resultados estadísticamente significativos en una prueba.
Un ejemplo puede ayudar a comprender este concepto y a aclarar la importancia de la potencia: supongamos que la conversión real (=población) de la página alternativa es efectivamente del 5%. La distribución muestral para la diferencia entre dos proporciones con conversión1=4%, conversión2=5% y n1=n2=5.000se representa en combinación con la distribución muestral mostrada anteriormente para la diferencia entre dos proporciones con conversión1=conversión2=4% y n1=n2=5.000 (figura 1).
Figura 2: distribuciones muestrales para la diferencia entre dos proporciones con p1=p2=0,04, n1=n2=5.000(línea roja) y p1=0,04, p2=0,05, n1=n2=5.000 (línea azul punteada), con una prueba unilateral y una fiabilidad de 0,95.
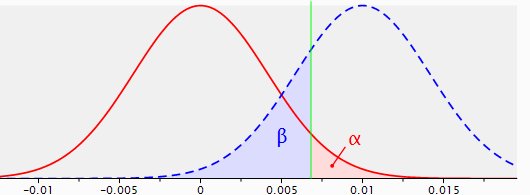
La línea azul punteada muestra la distribución muestral de la diferencia de tasas de conversión entre la original y la alternativa cuando en realidad (a nivel de población) la página original realiza un 4% de conversión y la página alternativa un 5%, con muestras de 5.000 cada una. La distribución muestral cuandoH0 es verdadera, la línea roja, se ha desplazado básicamente hacia la derecha. El valor modal de esta nueva distribución con el supuesto efecto del 1% es, por supuesto, del 1%, con desviaciones aleatorias tanto a la izquierda como a la derecha.
Ahora, todos los resultados, es decir, los resultados de las pruebas, a la derecha de la línea verde (que marca el área de significación) se consideran significativos. Todas las observaciones situadas a la izquierda de la línea verde se consideran no significativas. El área bajo la distribución «azul» a la izquierda de la línea de significación es beta, la probabilidad de no rechazar H0 cuando H0 no es en realidad cierta (una decisión falsa), y abarca el 22% de esa distribución.
Esto hace que el área bajo la distribución azul a la derecha de la línea de significación sea el área de potencia, y esta área cubre el 78% de la distribución muestral. La probabilidad de rechazar H0 cuando H0 no es cierta, es una decisión correcta.
Por tanto, la potencia de esta prueba específica con sus parámetros específicos es de 0,78.
En el 78% de los casos en que se realice esta prueba, se obtendrá un efecto significativo y, en consecuencia, se rechazará H0 . Podría ser aceptable, o quizá no lo sea; es una cuestión sobre la que deben ponerse de acuerdo el comercializador y el analista.
No es una cuestión sencilla, pero es importante. Supongamos, por ejemplo, que una expectativa de aumento del 10% en la conversión fuera realista, además de comercialmente interesante: 4,0% original frente al 4,4% de la alternativa. Entonces la situación cambia como sigue.
Figura 3: distribuciones muestrales para la diferencia entre dos proporciones con p1=p2=.040, n1=n2=5.000 (línea roja) y p1=.040, p2=.044, n1=n2=5.000 (línea azul punteada), con una prueba unilateral y una fiabilidad de .95.
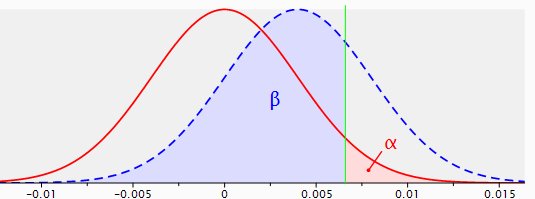
Ahora la potencia es de 0,26. En estas circunstancias, la prueba no tendría mucho sentido, de hecho es contraproducente, ya que la probabilidad de que dicha prueba conduzca a un resultado significativo es tan baja como 0,26.
Las cifras anteriores se han calculado y realizado con la aplicación «Gpower«:
Este programa calcula la potencia alcanzada para muchos tipos de pruebas, basándose en el tamaño de muestra deseado, el alfa y el efecto supuesto.
Del mismo modo, el tamaño requerido de la muestra puede calcularse a partir de la potencia deseada, el alfa y el efecto esperado, el alfa requerido puede calcularse a partir de la potencia deseada, el tamaño de la muestra y el efecto esperado, y el efecto requerido puede calcularse a partir de la potencia deseada, el alfa y el tamaño de la muestra.
Si se desea una potencia de 0,95 para un supuesto p1=0,040, p2=0,044, entonces los tamaños de muestra necesarios son 54,428 cada uno.
Figura 4: distribuciones muestrales para la diferencia entre dos proporciones con p1=p2=.040 (línea roja) y p1=.040, p2=.044 (línea azul punteada), utilizando una prueba unilateral, con una fiabilidad de 0,95 y una potencia de 0,95.
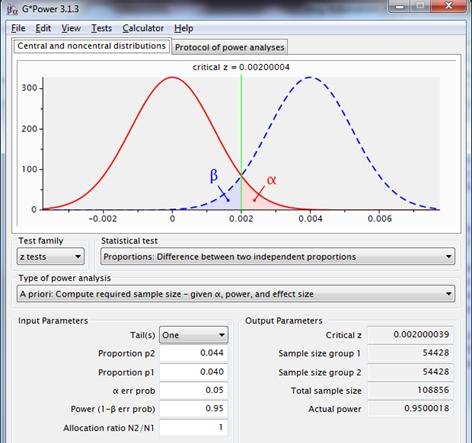
Esta figura muestra información omitida en los gráficos anteriores. También da una impresión de la interfaz del programa.
Descargar gratis: Guía de tests A/B
Aspectos importantes del análisis de potencia son la evaluación cuidadosa de las consecuencias de rechazar la hipótesis nula cuando la hipótesis nula es de hecho cierta -por ejemplo, basándose en los resultados de las pruebas se pone en marcha una campaña costosa suponiendo que será un éxito y ese éxito no se cumple- y las consecuencias de no rechazar la hipótesis nula cuando la hipótesis nula no es cierta -por ejemplo, basándose en los resultados de las pruebas no se pone en marcha una campaña, mientras que habría sido un éxito-.
Solución: ‘número predeterminado de conversiones’
El analista dice: haz un split con un mínimo de 100 conversiones por página competidora y una prueba unilateral con una fiabilidad de 0,95.
En el caso actual, con una conversión esperada de la página original del 4% y una conversión esperada de la página alternativa del 5%, se aconsejará un mínimo de 2.500 observaciones por página.
Sin embargo, cuando se somete a la prueba de potencia, este escenario demuestra una potencia de poco más de 0,5.
Figura 5: distribuciones muestrales para la diferencia entre dos proporciones con p1=p2=.04, n1=n2=2500 (línea roja) y p1=.04, p2=.05, n1=n2=2500 (línea azul punteada) utilizando una prueba unilateral, con una fiabilidad de 0,95.
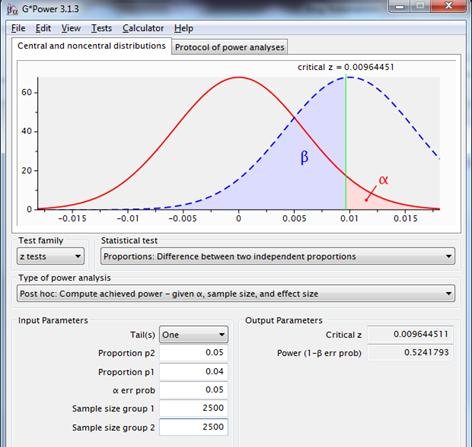
Para obtener una mayor potencia, debe haber un efecto mayor, debe elegirse una muestra de mayor tamaño o debe aumentarse alfa, por ejemplo a 0,2:
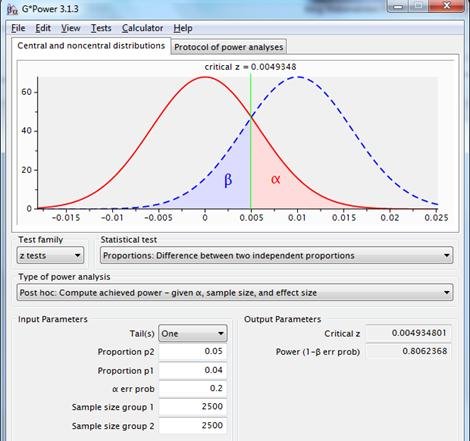
Un alfa de 0,2 devuelve una potencia de 0,8. La potencia es más aceptable; el «coste» de esta mayor potencia consiste en una mayor probabilidad de rechazar H0 cuando H0 es realmente cierta.
Una vez más, las consideraciones empresariales que implican el impacto de alfa y beta desempeñan un papel clave en tales decisiones.
El enfoque del «número de conversiones por defecto», con su regla empírica sobre el número de conversiones, en realidad pone una especie de límite a los tamaños de los efectos que aún tienen sentido someter a prueba (es decir, con una potencia razonable). En ese sentido, también supone una especie de estandarización, y eso en sí mismo no es un problema, siempre que se comprendan y reconozcan sus consecuencias.
Solución: ‘resultado significativo de la muestra‘
El analista dice: split test con suficientes observaciones para obtener un resultado estadísticamente significativo si en la prueba se produce realmente el supuesto efecto, prueba unilateral con una fiabilidad de 0,95.
Suena un poco raro, y lo es. Por desgracia, esta lógica se aplica a menudo en la práctica. El tamaño de muestra necesario se calcula básicamente suponiendo que el supuesto efecto se produce realmente en la muestra.
En el ejemplo utilizado: si en una prueba el original tiene una conversión del 4% y el alternativo del 5%, entonces serían necesarios 2.800 casos por grupo para alcanzar la significación estadística. Esto puede demostrarse con la sintaxis spss adjunta (limit at significant test result.sps).
Este tipo de cálculos son aplicados por diversas herramientas en línea que ofrecen calcular el tamaño de la muestra. Este enfoque ignora el concepto de error de muestreo aleatorio, ignorando así la esencia de la estadística inferencial y la comprobación de hipótesis nulas. En la práctica, siempre dará una potencia de 0,5 más un pequeño exceso adicional.
Figura7: distribuciones muestrales para la diferencia entre dos proporciones con p1=p2=.04, n1=n2=2800 (línea roja) y p1=.04, p2=.05, n1=n2=2800 (línea azul punteada), utilizando una prueba unilateral, con una fiabilidad de .95.
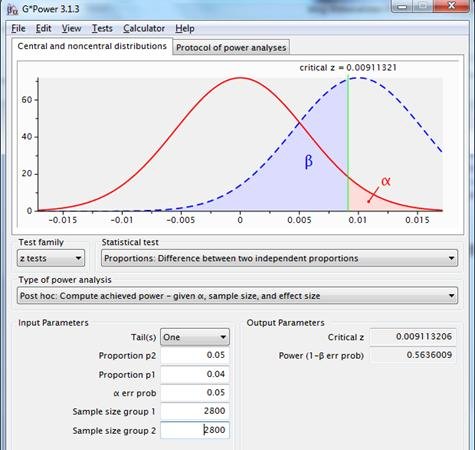
Con este sistema también se aplica una especie de normalización, concretamente sobre la potencia, pero ése no es el objetivo aparente para el que se inventó este método.
Solución: ‘fiabilidad y potencia por defecto‘
El analista dice: «Ejecuta la división con una potencia de 0,8 y una fiabilidad de 0,95 con una prueba unilateral».
En el caso actual, con un 4% de conversión para la página original frente a un 5% de conversión esperada para la página alternativa, alfa=0,05 y potencia=0,80, Gpower aconseja dos muestras de 5313.
Figura 8: distribuciones muestrales para la diferencia entre dos proporciones con p1=p2=.04(línea roja) y p1=.04, p2=.05 (línea azul punteada), utilizando una prueba unilateral con fiabilidad 0,95 y potencia 0,80.
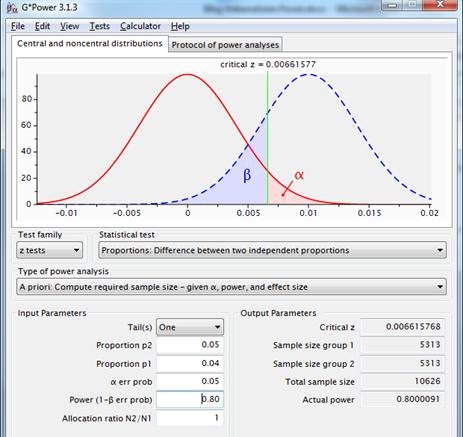
Este enfoque utiliza la fiabilidad deseada, el efecto esperado y la potencia deseada en el cálculo del tamaño de muestra necesario.
Ahora el analista tiene asidero en la probabilidad de que un efecto esperado/deseado/necesario conduzca a resultados estadísticamente significativos en una prueba, a saber, .8.
Algunas herramientas online, por ejemplo la Calculadora de Duración de Pruebas Divididas de VWO, utilizan el concepto de potencia en su cálculo del tamaño de la muestra.
En una presentación de VWO «Visitantes necesarios para tests A/B» se menciona una potencia de 0,8 como medida habitual.
Cabe preguntarse por qué debería ser una norma aceptable. ¿Por qué no se podría utilizar de forma más dinámica el tamaño de la potencia, así como el tamaño de la fiabilidad?
Solución: ‘fiabilidad y potencia deseadas‘
El analista dice: divide la carrera con la potencia y fiabilidad deseadas mediante una prueba unilateral.
Sigue una discusión sobre qué es una potencia y una fiabilidad aceptables en este caso, con como conclusión, digamos, ambas del 90%. Resultado según Gpower, 2 veces 5.645 observaciones:
Figura 9: distribuciones muestrales para la diferencia entre dos proporciones con p1=p2=,04 (línea roja) y p1=,04, p2=,05 (línea azul punteada), utilizando una prueba unilateral con fiabilidad=,90 y potencia=,90.
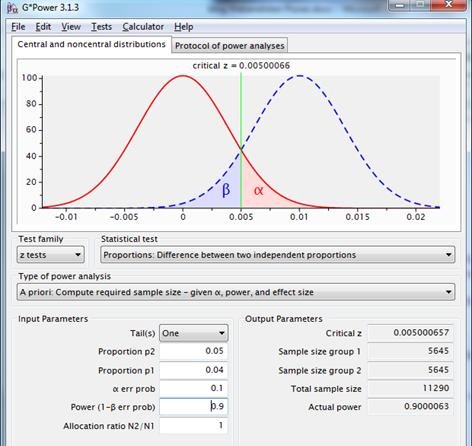
¿Y si el vendedor dice «Se tarda demasiado en reunir tantas observaciones»? Entonces la landing page dejará de ser importante. Hay espacio para un total de 3.000 observaciones de prueba. La fiabilidad es tan importante como la potencia. Es preferible realizar la prueba y tomar una decisión»?
Resultado sobre la base de esta restricción: fiabilidad y potencia ambas de 0,75. Si esto no plantea problemas a los interesados, la prueba puede continuar sobre la base de alfa=.25 y potencia=.75.
Figura 10: distribuciones muestrales para la diferencia entre dos proporciones con p1=p2=.04, n1=n2=1500 (línea roja), y p1=.04, p2=.05, n1=n2=1500(línea azul punteada), utilizando una prueba unilateral con igual fiabilidad y potencia.
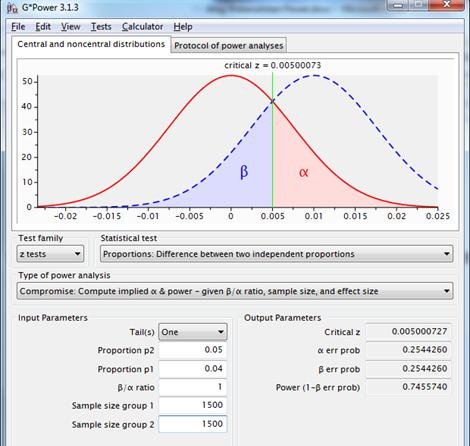
Este enfoque permite una elección flexible de la fiabilidad y la potencia. La consiguiente falta de normalización es una desventaja.
Conclusión
Existen múltiples enfoques para calcular el tamaño de muestra necesario, desde los de lógica cuestionable hasta los muy fundamentados.
Para los «experimentos cruciales» de importancia estratégica, se da preferencia al método más completo, en cuyo cálculo intervienen tanto «la fiabilidad deseada como la potencia». Si no hay posibilidad de contrastar efectos anteriores, se puede estimar un efecto utilizando un piloto con «tamaño de muestra por defecto» o «número de conversiones por defecto».
Para la mayoría de las decisiones a lo largo del año se recomienda «fiabilidad y potencia por defecto», por razones de comparabilidad entre pruebas.
Trabajar con los enfoques recomendados basados en el riesgo calculado conducirá a una optimización valiosa y a una toma de decisiones correcta.
Nota: Las capturas de pantalla utilizadas en el blog pertenecen al autor.
Preguntas frecuentes sobre el tamaño de la muestra de los tests A/B
Existen múltiples enfoques para determinar el tamaño de muestra necesario para los tests A/B. Para los «experimentos cruciales» de importancia estratégica, se da preferencia al método más completo, en cuyo cálculo intervienen tanto «la fiabilidad deseada como la potencia».
En el mundo online, las posibilidades de realizar tests A/B con casi cualquier cosa son inmensas. El tamaño de la muestra debe ser lo suficientemente grande como para demostrar con significación estadística que la versión alternativa es mejor que la original.







![Calculadora de significación estadística de tests A/B [Excel gratuito]](https://static.wingify.com/gcp/uploads/sites/3/2010/04/Feature-image_AB-Test-Statistical-Significance-Calculator-Free-Excel.png?tr=h-600)