O que é intervalo de confiança?
Em estatística, ao fazer qualquer tipo de estimativa, seja ela de resumo ou de teste, sempre existe uma incerteza, porque o número obtido é baseado em uma amostra limitada da população a ser estudada.
Suponha que uma pesquisa seja realizada para determinar o tempo médio que um medicamento leva para fazer efeito no tratamento de uma determinada doença. Ao monitorar alguns pacientes até o momento de sua recuperação, a duração de todo o processo é registrada para estimar uma média. Como essa estimativa é calculada a partir de dados de amostra limitados, haverá alguma incerteza associada a ela. O intervalo de confiança é o grau de incerteza em uma determinada métrica de interesse, normalmente uma média. Ele informa o grau de confiança de que os resultados de um experimento refletem o que se esperaria encontrar caso fosse possível obter os dados de toda a população.
Em termos estatísticos, o que é um intervalo de confiança?
Intervalo de confiança é o valor estimado de uma métrica com uma margem de erro. Trata-se do intervalo de valores em que se espera que sua estimativa se enquadre caso o teste seja refeito diversas vezes. O número de ocasiões em que a estimativa ficará dentro do intervalo dependerá do nível de confiança definido.
Se você tiver um intervalo de confiança com um nível de confiança de 95%, terá a certeza de que em 95 a cada 100 vezes a estimativa ficará entre os valores superior e inferior especificados pelo intervalo.
O nível de confiança desejado costuma ter relação com o nível estatístico (alfa) usado no teste da hipótese. Se você definir um alfa de 0,05, seu nível de confiança será 1 – 0,05 = 0,95 (95%).
Quando usar intervalos de confiança?
Toda vez que uma estimativa de estatística de teste é feita com dados de amostra, o intervalo de confiança é calculado para representar o grau de incerteza que existe com esses dados de amostra limitados. Isso ocorre porque as estimativas de pontos de amostra por si só não trazem nenhuma informação sobre a variação em torno do resultado, devido à limitação dos dados. Os intervalos de confiança são úteis para comunicar a possível variação que existe em torno de uma estimativa pontual.
Cálculo do intervalo de confiança
Intervalo de confiança é a terminologia mais presente nas estatísticas frequentistas. A maioria dos sistemas estatísticos informa o intervalo de confiança da estimativa juntamente com diversas estatísticas quando um teste é executado.
Para entender como calcular o intervalo de confiança, imagine que um grupo de analistas esteja interessado em determinar se as maçãs cultivadas em um pomar são grandes o suficiente para serem vendidas em uma loja on-line.
- Definição do número de amostras (N): os pesquisadores selecionam aleatoriamente 46 maçãs das árvores da fazenda. Portanto, N = 46.
- Cálculo da média dos dados de amostra: os pesquisadores descobrem que o peso médio (μ) das maçãs é de 86 gramas.
- Cálculo do desvio padrão (σ): é aconselhável usar o desvio padrão de toda a população. Entretanto, em muitos cenários, essa informação não está disponível. Se for o caso, o desvio padrão pode ser calculado a partir da amostra usando a seguinte fórmula:
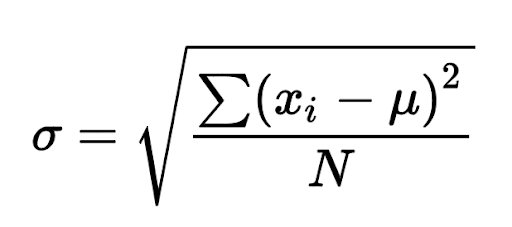
- Definição do nível de confiança que será usado: pesquisas de mercado costumam usar um nível de confiança de 95% a 99%. Digamos que os pesquisadores do nosso exemplo tenham decidido usar um nível de confiança de 95%.
- Obtenção do valor Z: de acordo com o nível de confiança selecionado, é preciso obter o valor Z, conforme especificado na tabela abaixo.
| Nível de confiança | Z |
| 80% | 1.282 |
| 85% | 1.44 |
| 90% | 1.645 |
| 95% | 1.96 |
| 99% | 2.576 |
| 99.50% | 2.807 |
Essencialmente, o valor Z é o intervalo que tem uma curva de distribuição padrão igual ao nível de confiança definido.
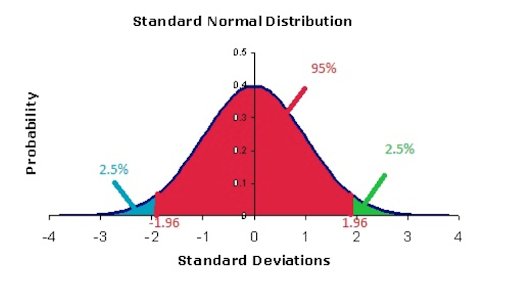
Para o nível de confiança de 95%, o valor Z é igual a 1,960.
6. Cálculo do intervalo de confiança: para calcular o intervalo, usamos a fórmula a seguir.
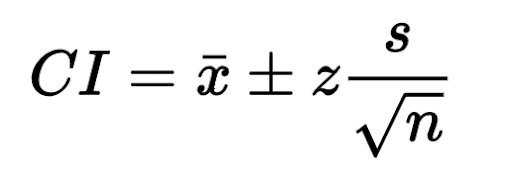
CI = 86 ± 1,960 (6,2/6,782)
Essa fórmula apresenta o resultado 86 ± 1,79 como o intervalo de confiança.
7. Conclusão: os pesquisadores determinaram que a média da amostra (46 maçãs) provavelmente (com 95% de confiança) está entre 84,21 gramas e 87,79 gramas. Se o peso necessário para que as maçãs estejam adequadas para serem vendidas na loja on-line for menor que o limite inferior do intervalo de confiança estimado, elas serão aprovadas para venda.
Cuidado ao usar intervalos de confiança
O intervalo de confiança não sugere que o “valor verdadeiro” da sua estimativa está dentro dos limites do intervalo. A interpretação correta é que há uma chance de 95% de que o intervalo de confiança calculado contenha a faixa de estimativas que se espera obter se o experimento for repetido diversas vezes. Com o aumento dos dados, a chance de o intervalo de confiança incluir o valor real da estimativa também cresce.
Na VWO, adotamos a metodologia bayesiana, em que intervalos de credibilidade são usados para projetar a incerteza em torno da estimativa. O conceito bayesiano de um intervalo de credibilidade é mais prático e interpretável do que o intervalo de confiança. Para um intervalo de credibilidade de 95%, o “valor verdadeiro” da métrica que você deseja estimar tem uma probabilidade de 95% de estar dentro do intervalo.
Para entender nossos relatórios em detalhes, faça um teste grátis ou solicite uma demonstração com os nossos especialistas em produtos.