Bayesiano

O que é teoria bayesiana?

Bayesiano é um dos dois conjuntos mutuamente exclusivos de fundamentos estatísticos (o outro é a inferência frequentista) que podem ser usados para modelar qualquer problema estatístico. Os bayesianos consideram que o parâmetro de interesse é subjetivo (uma distribuição de possibilidades), descrito por uma distribuição de crenças que é atualizada com a observação dos dados. 

Já os frequentistas consideram que o parâmetro de interesse é objetivo (uma estimativa verdadeira) e se baseiam em múltiplas amostragens para chegar mais perto do valor verdadeiro do parâmetro. Para entender e apreciar melhor o contraste entre as duas escolas de pensamento, é necessário fazer um estudo aprofundado e comparativo entre a estatística bayesiana e a estatística frequentista.

A abordagem bayesiana permite que um analista incorpore sua crença na pesquisa ao estimar um parâmetro de interesse. Ela fornece uma estrutura em que o analista pode começar com uma crença prévia e, à medida que mais dados são coletados, essa crença é atualizada. A integração da crença prévia com os dados disponíveis é realizada usando o teorema de Bayes.

Pense em um estudo para estimar a altura média dos brasileiros. Um estatístico pode ter a crença prévia de que a altura dos brasileiros está distribuída entre 50 cm e 2,50 m. O estudo envolveria medir a altura de vários indivíduos e, conforme mais observações fossem feitas, essa distribuição se concentraria na altura média entre eles.

A importância da metodologia bayesiana

As metodologias bayesianas são úteis na estimativa de parâmetros quando a coleta de dados para a construção de modelos é complexa e a tomada de decisões precisa ser feita com dados limitados. Quando há tamanhos grandes de amostra, as metodologias bayesianas frequentemente apresentam resultados semelhantes aos produzidos pelos métodos frequentistas. 

Em testes de hipóteses, é muito mais fácil interpretar os resultados obtidos com o método bayesiano do que com seu equivalente frequentista. Na visão bayesiana, trabalhamos com um grau de certeza, que é a probabilidade de que o valor verdadeiro de um parâmetro esteja dentro do intervalo estimado. Essa probabilidade combina nosso conhecimento prévio com os dados disponíveis. É essa noção de probabilidade que a diferencia da abordagem frequentista, na qual não existe grau de certeza. Uma hipótese pode ser escolhida após uma avaliação de risco baseada nesse grau de certeza em relação à estimativa posterior.

O que é inferência bayesiana?

O termo “inferência bayesiana” se refere ao ato de atualizar seu conhecimento à medida que novos dados surgem. Nessa abordagem, você raramente tem certeza de um resultado. No entanto, você pode ter algum grau de confiança e, dependendo dele, tomar uma decisão. É simples assim.

Na estatística bayesiana, todos os parâmetros observados e não observados em um modelo estatístico estão associados a distribuições de probabilidade, classificadas como “distribuição a priori” e “distribuição dos dados”. O fluxo de trabalho bayesiano costuma envolver as três etapas a seguir: 

• escolher uma distribuição a priori apropriada que capture o conhecimento disponível sobre um parâmetro em um modelo estatístico. Normalmente, ela é determinada antes do processo de coleta de dados; 
• escolher uma função de verossimilhança usando as informações sobre os parâmetros disponíveis e os dados observados;
• combinar tanto a distribuição a priori quanto a função de verossimilhança usando o teorema de Bayes para obter a distribuição a posteriori dos parâmetros.

A distribuição a posteriori reflete o conhecimento atualizado ao combinar o conhecimento prévio com os dados observados. Ela é usada posteriormente para conduzir inferências.

No caso de um teste A/B, ao calcular a distribuição a posteriori para cada variante, podemos expressar a incerteza sobre nossas crenças por meio de declarações probabilísticas. Por exemplo, podemos perguntar: “Qual é a probabilidade de que, para uma determinada métrica de interesse, a variante A tenha um valor maior que a variante B?”. Resultados interpretáveis ajudam os analistas a desenvolver insights informativos e compartilhá-los com colegas para que possam tomar decisões ideais em cenários comerciais complexos.

Forças do método bayesiano

• Oferece uma forma fundamentada e natural de combinar o conhecimento de um domínio com os dados. É possível incorporar informações de experimentos passados sobre um parâmetro e formar uma distribuição a priori para experimentos futuros. Com novas observações, as distribuições a posteriori dos experimentos passados podem servir como a atual distribuição a priori para obter a nova distribuição a posteriori.
• Oferece respostas interpretáveis. Por exemplo: “Há uma probabilidade de 0,9 de que o parâmetro verdadeiro esteja dentro de um intervalo confiável de 90%”.
• Oferece uma estrutura natural para uma ampla gama de modelos paramétricos, como modelos hierárquicos e problemas com dados ausentes. O MCMC, junto com outros métodos numéricos, fornece um design computacional viável para todos os modelos paramétricos.
• Não requer dados mínimos. Diferentemente dos métodos frequentistas, não é necessário ter um número mínimo de dados para trabalhar com uma metodologia baseada na estatística bayesiana. Como o conceito de incerteza já está embutido no sistema bayesiano, as métricas obtidas continuam válidas.

Limitações do método bayesiano

• A escolha da distribuição a priori não é padronizada. Não há uma maneira definida para escolhê-la. São necessárias habilidades especializadas para traduzir crenças subjetivas em uma distribuição a priori formulada matematicamente. Os resultados obtidos podem ser enganosos se a distribuição a priori escolhida não fizer sentido. 

• Quando há poucos dados, as distribuições a posteriori são fortemente influenciadas pelas distribuições a priori. Do ponto de vista prático, isso pode gerar debates se não houver consenso sobre a validade da distribuição a priori escolhida.

• Metodologias bayesianas frequentemente têm um custo computacional alto, especialmente quando há um grande número de parâmetros envolvidos. Apesar disso, ao longo dos anos, surgiram muitas metodologias bayesianas eficientes para casos de uso específicos.

Como a VWO utiliza o método bayesiano?

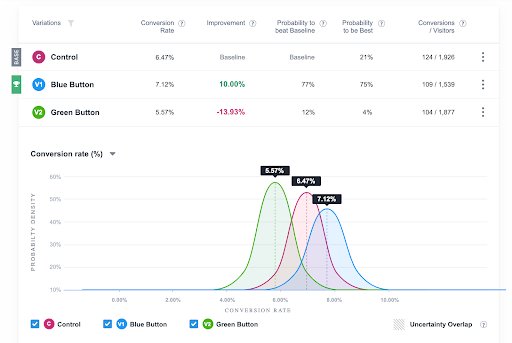
A VWO é alimentada por um motor estatístico bayesiano, em que os parâmetros de cada variante de um teste A/B estão ligados a uma distribuição de probabilidade. À medida que os dados são observados no teste, essas distribuições são atualizadas usando o teorema de Bayes. Calculamos as métricas de decisão exibidas em nosso relatório usando essas distribuições atualizadas. Consulte o whitepaper da VWO para entender a matemática por trás da nossa modelagem bayesiana. Você também pode fazer um teste gratuito de 30 dias para explorar nossos relatórios detalhados.