O que é erro do tipo II?
Imagine que uma empresa queira aumentar o número de usuários de seu produto.
Para chegar ao objetivo, ela cria a hipótese de que oferecer um teste grátis poderá incentivar os usuários a experimentar o produto e avaliá-lo de acordo com suas necessidades. Para validar essa hipótese, a empresa faz um teste A/B com duas estratégias: oferecer um teste grátis e não oferecer a opção de teste ao público. Depois de executar o experimento por um determinado período, o resultado declarado não é significativo. Como o teste não fornece evidências fortes para as hipóteses propostas, ele é rejeitado, e a empresa decide descontinuar a oferta do teste grátis.
Agora, imagine que, na realidade, os resultados do teste estivessem errados e a oferta de testes grátis tenha aumentado o número de usuários do produto. Nesse caso, o experimento apresentou um falso negativo ou erro do tipo II. Se um teste A/B ou multivariado declara um resultado sem significância estatística quando existe diferença no desempenho das variações, há um erro do tipo II.
Em termos científicos, durante o processo de teste da hipótese, se um teste não rejeita a hipótese nula (que representa nenhum efeito) quando ela é falsa e deveria ser rejeitada, ocorre o chamado erro do tipo II ou falso negativo. Uma hipótese nula é definida antes do início de um teste A/B ou multivariado, o que indica que não há diferença entre as variações testadas.
Por que é importante entender os erros do tipo II?
Cada erro do tipo II pode representar uma oportunidade perdida de inovar e, potencialmente, aumentar o número de conversões a longo prazo. Uma grande quantidade de erros do tipo II pode levar à perda de muitas ideias boas que poderiam promover o crescimento dos negócios.
Causas do erro do tipo II
Erros do tipo II têm uma relação inversa com o poder estatístico de um teste. Um alto poder estatístico apresenta um baixo número de erros do tipo II. Poder estatístico é a probabilidade de um teste de hipótese detectar uma diferença estatística na taxa de conversão entre as variações, se houver um efeito a ser identificado.
O poder estatístico e a diferença mínima que você considera relevante determinam juntos o tamanho da amostra de um teste. Um poder estatístico maior e um tamanho de efeito menor podem exigir um tamanho de amostra maior, o que resulta em um teste com duração mais longa.
Um teste tem pouco poder se for interrompido precocemente, o que pode levar a um elevado número de erros do tipo II. Isso dificulta a detecção de verdadeiros positivos, mesmo se houver grandes efeitos.
Nos testes A/B ou multivariados, há uma compensação entre a precisão estatística e a duração do teste. Dependendo da diferença de taxa de conversão estrategicamente adequada para o seu negócio e do poder estatístico, é possível determinar o tamanho viável da amostra a ser coletada para a realização do teste.
Representação gráfica do erro do tipo II
Veja abaixo a representação de um modelo de hipótese nula e de um modelo de hipótese alternativa.
- O modelo nulo representa as probabilidades de obter todos os resultados possíveis se o estudo fosse repetido com novas amostras e a hipótese nula fosse verdadeira na população.
- O modelo alternativo representa as probabilidades de obter todos os resultados possíveis se o estudo fosse repetido com novas amostras e a hipótese alternativa fosse verdadeira na população.
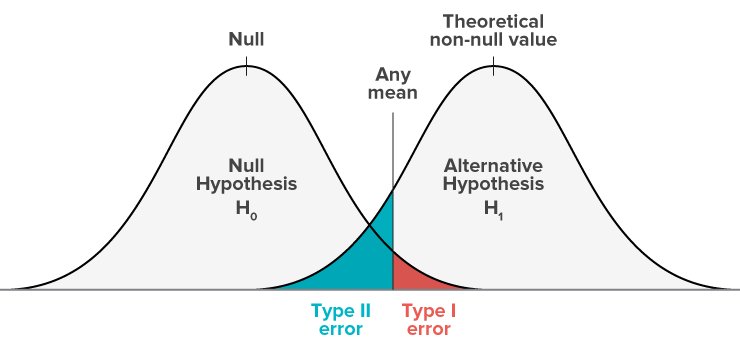
A área sombreada é chamada de região crítica. Se os seus resultados estiverem na região crítica azul dessa curva, eles serão considerados estatisticamente não significativos e a hipótese nula não será rejeitada. Entretanto, essa é uma conclusão falsa negativa, pois a hipótese nula é falsa em casos como esse.
A compensação entre os erros do tipo I e do tipo II
Em estatística, as taxas de erro do tipo I e do tipo II afetam uma à outra. Os erros do tipo I dependem do nível de significância estatística que afeta o poder estatístico de um teste. O poder estatístico é inversamente relacionado à taxa de erro do tipo II.
Isso significa que há uma compensação entre os erros do tipo I e do tipo II:
- Um nível de significância baixo diminui o risco de erro do tipo I, mas aumenta o risco de erro do tipo II.
- Um teste com poder elevado pode ter um risco menor de erro do tipo II, mas apresentar um risco alto de erro do tipo I.
Os erros do tipo I e do tipo II ocorrem quando as distribuições das duas hipóteses se sobrepõem. A área sombreada em vermelho representa alfa, a taxa de erro do tipo I, e a área sombreada em azul representa beta, a taxa de erro do tipo II.
Portanto, ao definir a taxa de erro do tipo I, você também influencia indiretamente a taxa de erro do tipo II.
Como controlar o erro do tipo II?
Ao aumentar o poder estatístico do seu teste, você consegue reduzir o risco de que um erro do tipo II ocorra. É possível aumentar o poder estatístico das seguintes formas:
- Aumento do tamanho da amostra
Com o aumento do tamanho da amostra, as chances de identificar diferenças ao testar uma hipótese crescem, o que resulta no aumento do poder do teste.
- Aumento do limite do nível de significância
A maioria dos testes estatísticos usa 0,05 como nível de significância para determinar um resultado estatisticamente significativo. Ao aumentar o nível de significância, você terá mais chances de rejeitar a hipótese nula quando ela for verdadeira.
Ao aumentar a probabilidade de rejeitar as hipóteses nulas, você diminui os erros do tipo II, mas eleva as chances de que erros do tipo I ocorram. Portanto, é preciso avaliar o impacto dos erros do tipo I e do tipo II para definir um nível de significância apropriado.
Na VWO, usamos a probabilidade de ser a melhor (PBB) e a perda potencial absoluta (PL) como métricas de tomada de decisão para determinar uma variação vencedora. A métrica PBB sinaliza a vantagem que uma variação tem em relação às variações concorrentes. Manter um nível de PBB mais alto pode reduzir o número de erros do tipo II.
Para saber mais sobre como a VWO ajuda você a reduzir o número de erros, faça um teste grátis ou solicite uma demonstração com um de nossos especialistas em otimização.