Erro do tipo I

O que é erro do tipo I?

Imagine uma situação em que uma empresa de comércio eletrônico deseja aumentar suas vendas atuais. Para isso, é criada a hipótese de que, ao otimizar o design da página do produto, a taxa de checkout tende a melhorar, o que resultaria em um maior número de compras.

Para validar essa hipótese, a empresa realiza um teste A/B com dois designs e monitora a taxa de cliques no botão de checkout. De acordo com a abordagem de teste de hipótese do teste A/B, depois de executar o experimento por um determinado período, se ele declarar um resultado com significância estatística a favor do novo design da página do produto, a nova hipótese será considerada verdadeira.

Mas suponha que os resultados do teste estejam errados e que não haja nenhuma diferença entre os dois designs. Neste caso, o teste cometeu um falso positivo ou erro do tipo I. Se um teste multivariado ou A/B declara um resultado com significância estatística quando, na realidade, não existe diferença no desempenho das variações que estão sendo testadas, há um erro do tipo I.

Em termos científicos, durante o processo de teste da hipótese, se uma hipótese nula (que representa nenhum efeito) é rejeitada, mesmo quando ela está correta e não deva ser rejeitada pelo teste, ocorre o chamado erro do tipo I ou falso positivo. Uma hipótese nula é definida antes do início de um teste A/B ou multivariado, o que indica que não há diferença entre as variações testadas.

Em termos mais formais, em um teste A/B, se duas variações forem semelhantes e não afetarem a métrica que está sendo testada de formas distintas, poderá ocorrer um erro se a hipótese nula for rejeitada após a conclusão do teste. Neste caso, se for determinado que há uma diferença estatística entre as variações, haverá um erro do tipo I.

Por que é importante entender os erros do tipo I?

Imagine que, depois de executar um teste A/B, você chegue à conclusão incorreta de que a variação B é a vencedora e a implemente para que seja exibida a todos os usuários. Esse tipo de conclusão equivocada pode ser prejudicial para a taxa de conversão de uma empresa e resultar na perda de receitas. Portanto, sempre que executar um teste A/B, é fundamental compreender os erros do tipo I para:

• Estimar os riscos se houver uma conclusão incorreta

Realizar experimentos de forma cientificamente disciplinada

O que causa um erro do tipo I?

Ao realizar um teste estatístico, sempre há a possibilidade de ocorrer um erro do tipo I, pois as estimativas são feitas com base em uma amostra limitada de dados. Um teste estatístico não promete apresentar as decisões corretas todas as vezes, mas tende a oferecer as melhores opções na maioria delas. Por isso, uma metodologia de teste deve ser avaliada com base em sua capacidade de restringir os erros a um determinado limite.
Os erros do tipo I são causados por dois motivos principais:

• Aleatoriedade: em um teste de hipótese, o analista usa apenas uma pequena parte da população dos dados para fazer estimativas. Portanto, existe a possibilidade de que, em determinados casos, as amostras coletadas não representem a população real, levando a conclusões incorretas.
• Conclusão antecipada de um teste: no método frequentista, espera-se que o teste de hipótese seja realizado após a coleta do tamanho desejado da amostra necessária para o estudo. Entretanto, em muitas ocasiões, os testes são encerrados assim que o valor-p fica abaixo do limite definido. Isso leva a uma taxa elevada de falsos positivos.

Representação gráfica da taxa de erro do tipo I

Veja abaixo a representação de um modelo de hipótese nula e de um modelo de hipótese alternativa.

• O modelo nulo representa as probabilidades de obter todos os resultados possíveis se o estudo fosse repetido com novas amostras e a hipótese nula fosse verdadeira na população.
• O modelo alternativo representa as probabilidades de obter todos os resultados possíveis se o estudo fosse repetido com novas amostras e a hipótese alternativa fosse verdadeira na população.

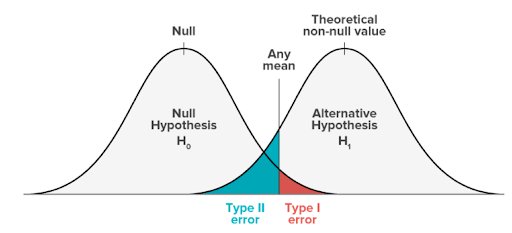
A área sombreada é chamada de região crítica. Se os seus resultados estiverem na região crítica vermelha dessa curva, eles serão considerados estatisticamente significativos e a hipótese nula será rejeitada. Entretanto, essa é uma conclusão falsa positiva, pois a hipótese nula é de fato verdadeira nesses casos.

A compensação entre os erros do tipo I e do tipo II

Em estatística, as taxas de erro do tipo I e do tipo II afetam uma à outra. Os erros do tipo I dependem do nível de significância estatística que afeta o poder estatístico de um teste. O poder estatístico é inversamente relacionado à taxa de erro do tipo II.

Isso significa que há uma compensação entre os erros do tipo I e do tipo II:

• Um nível de significância baixo diminui o risco de erro do tipo I, mas aumenta o risco de erro do tipo II.
• Um teste com poder elevado pode ter um risco menor de erro do tipo II, mas apresentar um risco alto de erro do tipo I.

Os erros do tipo I e do tipo II ocorrem quando as distribuições das duas hipóteses se sobrepõem. A área sombreada em vermelho representa alfa, a taxa de erro do tipo I, e a área sombreada em azul representa beta, a taxa de erro do tipo II.

Portanto, ao definir a taxa de erro do Tipo I, você também influencia indiretamente o tamanho da taxa de erro do Tipo II.

Como controlar os erros do tipo I?

A chance de cometer esse erro está relacionada ao nível de significância (alfa ou α) que você define.

Esse valor, estabelecido no início do estudo, avalia a probabilidade estatística de obtenção dos resultados (valor-p). O termo “valor-p” é usado principalmente na abordagem estatística frequentista.

De acordo com a literatura acadêmica, o nível de significância costuma ser definido como 0,05 ou 5%. Isso significa que, a cada 100 testes em que as variações são as mesmas, cinco deles devem informar que as variações são estatisticamente diferentes. Se o valor-p obtido em seu teste for menor do que o nível de significância definido, haverá uma sinalização de que a diferença é estatisticamente significativa e consistente com a hipótese alternativa. Por outro lado, a diferença não será estatisticamente significativa se o valor-p for maior do que o nível de significância.

Para reduzir a probabilidade de ocorrência do erro do tipo I, basta definir um nível de significância mais baixo e executar os experimentos por mais tempo para coletar mais dados.

Na VWO, usamos a probabilidade de ser a melhor (PBB) e a perda potencial absoluta (PL) como métricas de tomada de decisão para determinar uma variação vencedora. O uso da métrica PL combinada com PBB garante que, mesmo que ocorra um erro do tipo I, o impacto geral causado pela decisão equivocada seja tolerável para a empresa.

Para saber mais sobre como a VWO ajuda você a reduzir o número de erros, faça um teste grátis ou solicite uma demonstração com um de nossos especialistas em otimização.