The Frequentists, The Bayesians and The Epistemologists

The Frequentist and the Bayesian are two opposing schools of thought in statistics and both have a unique approach to solve the problems of randomness. Statisticians have tried to explain the difference between the approaches for decades. Statistical cartoonists and meme makers have had a feast over the debate for years. There seems to be no absolute consensus about which one is better or even what exactly is the difference between the two. There are the opinionists, who have chosen a side and vocally criticize the other. Then there are the agnostics, who conveniently mix up the best of both sides. And finally there are the epistemologists, who have abandoned the debate calling it an unnecessary statistical complication and chosen to study a higher question, “Where does knowledge come from?” (Epistemology is the branch of philosophy that studies the nature and origins of knowledge.)

A statistician might tell you that Frequentists believe that the true mean of a random process is an unknowable single point estimate. Hence, Frequentists rely on repeatedly sampling data from the process and trying to narrow down the range of the true value (hence the term ‘frequent-ists’). Bayesians, on the other hand, believe in modeling and specifying the underlying data generating process. Hence, they start by specifying the model with the underlying parameters as random variables. As samples are gathered, they update their beliefs about the underlying model. Unlike the Frequentists, they express the true mean of the process as a probability distribution rather than a single point estimate.

But the epistemologist contradicts both the Frequentist and the Bayesian by asking, what is the source of knowledge and how does it differ? In practice if you have observed some data, then there can only be some fixed piece of knowledge that can be extracted from this evidence. This knowledge is the fundamental source of statistical inference and cannot differ based on the statistical viewpoint. The epistemologist hence rejects the debate as a statistical hallucination and moves ahead. 

From the perspective of statistical significance, VWO’s opinion on the debate has continuously evolved over the past few years. We have come to realize that the distinction between the two schools is deeper. In a nutshell, Frequentists consider any prior beliefs about the data-generating process to be a bias and follow a pure evidence based approach to judge if an effect is significant. Bayesians on the other hand acknowledge the role of the data generating process in statistical inference and hence give an answer based on prior beliefs and evidence.

The Difference in Direction of Probabilities

The fundamental difference between Bayesians and Frequentists is that Bayesians try to work in a framework of backward probabilities where they directly ask what is the probability of different causes after taking evidence into account. Frequentists on the other hand, work only with forward probabilities. They make an expected hypothesis and then judge if the evidence supports the assumed hypothesis or not. The two types of probabilities have been explained in detail in the previous blog post.

The difference in approach and the information they use directly originates from the way they have framed their query. Observe the following questions in the context of an A/B test.

1. (Frequentist, Forward Probability) How surprising is the evidence assuming that the control and the variation are the same (the null hypothesis)?

2. (Bayesian, Backward Probability) What is the chance that variation is better than the control having observed the data from the test?

To understand further let me walk you through a thought experiment. Imagine yourself to be an experimenter trying to test their hypothesis. Your hypothesis can be a good hypothesis that actually impacts customer behavior. Or it can be a bogus hypothesis which might win the experiment but will eventually wear off. You can get a winner with some probability from both a good hypothesis and a bad hypothesis. If the hypothesis is good, you will get a winner 80% times. But even if the hypothesis is bogus, you will get a winner 5% times.

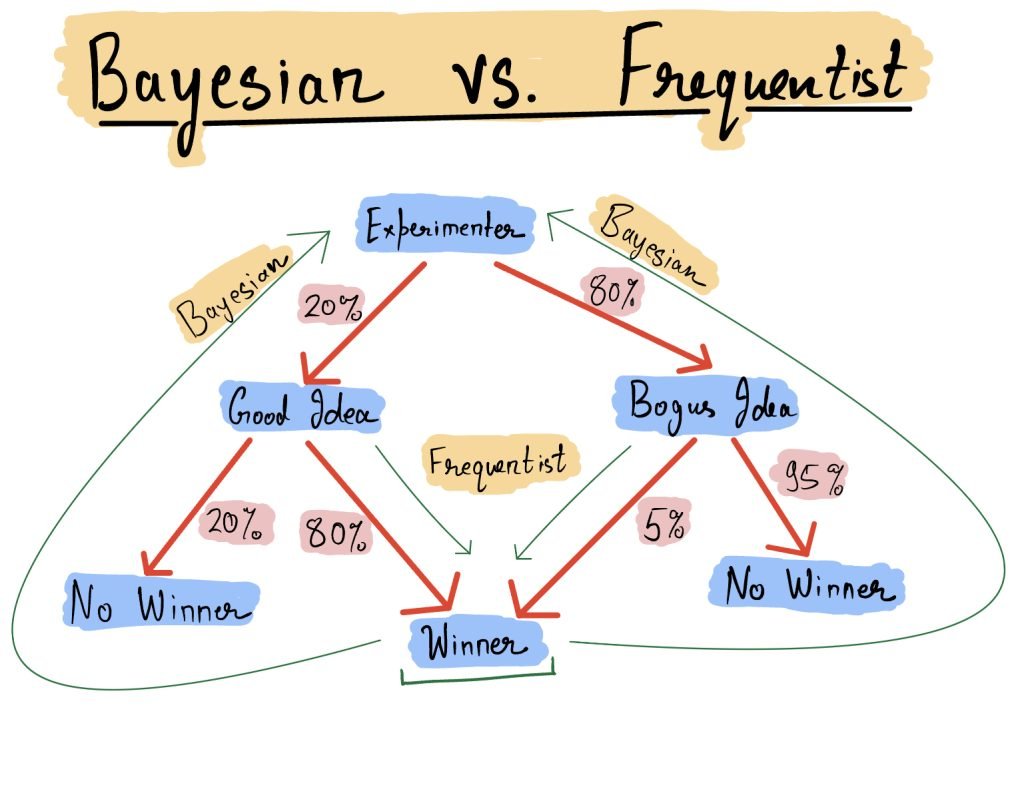
Observe the difference in the direction of the queries. To understand the difference better, let us consider the aspect of how each school of thought expresses the aspect of statistical accuracy. Imagine you have been running 100s of experiments and want to get a probabilistic estimate on how often a test result is wrong. 

The questions on statistical accuracy can also be framed in two distinct ways depending on the direction of probabilities.

1. (Frequentist, Forward Probability) If there is no improvement in the test (bogus idea), what is the chance that the test results in a winner? This is also called the False Positive Rate. In the example above, this is 5% (the edge from Bogus Idea to Winner).

2. (Bayesian, Backward Probability) If you have gotten a winner in the test, what is the chance that the hypothesis was actually bogus? This is also called the False Discovery Rate. In the example above, to calculate you need to use the Bayes Rule and see how likely it is to get a winner from both routes. The proportion of probability from the bogus route is the answer. Hence, 4%/(4% + 16%) = 20%. (to understand this calculation, see the Burglar problem in the previous post)

Interestingly, the Bayesian question cannot be answered without the information on the 20%-80% split between good and bogus ideas. This is precisely the extra piece of knowledge that the Bayesians include in their answer. It is called the base rate.

The Base Rates and Evidences

There are two important pieces of knowledge that can be used in statistical inference. But which pieces of information get used depend on the type of question being asked. 

1. Evidence: Evidence comes from three main properties of the observed sample: the uplift, the standard deviation and the sample size. It has been explained as a measure of surprise in a previous post. 

2. Base Rates: Base rate is the proportion of good ideas that an experimenter generates and as explained it influences the accuracy of a statistical inference. This is the upper edge information in the drawing above. It’s impact on statistical accuracy has been explained in another post. 

The primary difference between Frequentists and the Bayesians lies in the use of base rates. Frequentists ask a forward probability question that blocks the effect of the base rate by design. Hence, they only use evidence to make a statistical inference. The Bayesians on the other hand ask a backward probability question and by design need both the base rate and the evidence to give the correct answer.

However, base rates and evidence have a chicken and egg problem to them. Base rates are nothing but a meta-summarisation of all prior evidence. To understand, imagine that you are an experimenter at Amazon and you want to estimate your base rate of generating a good idea. To estimate your base rates, you need to look at the proportion of wins from your experimentation journey uptill now. Suppose that Amazon is already so optimized that in reality you are only able to generate only 1 in 100 good ideas. If your false positive rate is 5%, then you are getting 6 winners in 100 tests out of which 5 are false positives and 1 is the truly good idea you generated. Your evidence in this case will be severely flawed as 5 out of 6 of your winners are false (and you have no way to know it). How will you estimate your true base rates in such a case?

Hence, estimating true base rates is hard and the eventual argument between the Bayesians and Frequentists boils down to how much belief and how much evidence to rely on when making statistical inference.

Conclusion

In light of the difficulty to estimate base rates, Bayesians have developed the uninformative prior (a zero information base rate) which leads Bayesian inferences to rely purely on evidence, just like their Frequentist counterparts. In practice hence, Bayesian and Frequentist methods of statistical inference give the same result unless an informative prior is put in place. The epistemologist hence mocks the entire Bayesian vs Frequentist debate as a meaningless exercise.

We at VWO, after reflecting on all our learnings in statistics, have built an engine that is Bayesian by design. We acknowledge the difficulty in determining base rates and hence run our approach with an uninformative prior that aligns our inferences with their Frequentist counterparts.

However, defining the data-generating process in a Bayesian way has given us a stronger flexibility in interpreting our statistical results compared to the Frequentist way. This has in turn allowed us to extract inferences from data that provide more practical value to the customer. Further, by giving an inlet to define prior beliefs, our Bayesian approach has the potential to be more accurate if a good approximation to base rates can be made.

In the next few posts, I will detail out both approaches in detail, their limitations and take you through the journey of how we built an advanced Bayesian A/B testing engine.