The Forward Probability and The Backward Probability

In 1999, a lady named Sally Clark was wrongly convicted of murdering her two infants. The first child had died in 1996, just under three months of age. The second child had died in 1997, at 2 months of age. The prosecution got an expert from the field of child abuse, Professor Roy Meadow. Meadow claimed based on a recent study that in a house with no smokers, a middle-aged mother and an earning member, the chance of a sudden infant death is 1 in 8543. So, the chance of two sudden infant deaths is 1 in 73 million (squared). The prosecution then claimed this provides very strong evidence that Clark was guilty of murdering her own two sons. The fallacy of the argument is now widely understood as the Prosecutors’ fallacy.
The Prosecutors’ fallacy is when a prosecutor makes the claim that the “innocent” explanation of a crime is so improbable that the “guilty” explanation must be the correct one. However, statistically it is possible that the probability of the “guilty” explanation is even lower. We make the error that we automatically assume that “innocent” and the “guilty” probabilities need to sum up to 1. This is an error we often make when dealing with events of a very rare occurrence.
The jury failed to realize that the base rate of a mother killing her two infant sons without motive was extremely low. Base Rates are the prevalence of an effect in the overall population and is a concept that applies to all tests of statistical inference. Base rates and why they matter have been explained in detail in the previous blogpost of this series.
In this blogpost, I take you deeper into the discussion of where base rates matter. One part of all statistical questions flow forward in time and forward in causality. They ask questions about what will happen in the future based on what has happened today. The other part flows backward in time and backward in causality. They ask questions about the past on what is likely to have happened in the past based on what has happened today. These are the two types of probabilities and in terms of information, base rates are the difference between the two.
The Two Types of Probabilities
The two types of probabilistic queries are directionally opposite to each other in the flow of time and causality. Let us review both.
- The Forward Probability: Consider these questions. What is the chance of rain tomorrow given it is cloudy today? What is the chance that Bob will win a poker hand if he starts with two aces? What is the chance that an A/B test declares a winner if there was no change made to the webpage? All these questions are anticipatory in nature. They are forward probability questions because they condition on the cause and ask the probability of an effect. In other words, they go from the past to the future.
- The Backward Probability: Now consider their backward counterparts and reflect on how they are different. What is the chance that yesterday was cloudy, given that it has rained today? What is the chance that Bob started with two aces given that he has won the hand? What is the chance that there was actually no impact on the goal metric given the A/B test has declared the winner? Observe the retrospective nature of these questions. They are backward probability questions because they condition on the effect and ask the probability of the cause. In other words, they go back from the future to the past.
The difference might seem nuanced but it is far harder to calculate backward probabilities than their forward probability counterparts. In fact until Thomas Bayes gave us the Bayes Rule in the 18th century, there was no way to calculate backward probabilities at all. Further, before the invention of computers backward probabilities were very hard to calculate (for reasons we will see next). With new age computing power, backward probabilities can be easily calculated and the distinction between is becoming meaningful in statistics.
Forward Probabilities have been used more often through history and forms the basis of the Frequentist school of thought. Backward Probabilities have had a revival in the 21st century and forms the basis of the Bayesian School of Thought.

The Burglar and The Bayes Rule
A simple example will help you understand the complexity with backward probabilities. Suppose that there are only two ways in which a burglar can enter your home. The front door has a camera and hence the chance of a break in from the front door is 5%. The backdoor is towards the forest and hence the chance of a break in from the back door is 10%. Assume for simplicity that everyday a burglar tries to break in and he chooses the front door with a 20% chance and the back door with an 80% chance.
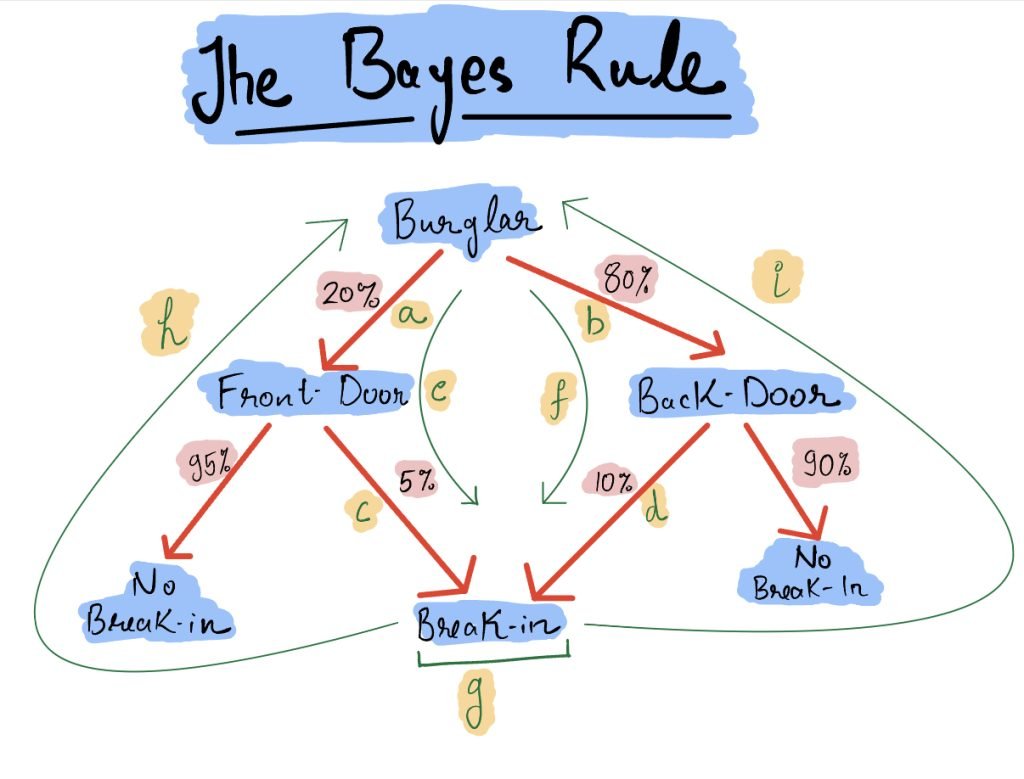
Let us pose a few questions of probability in the above situation
| Index | Type | Question | Expr | Answer |
| a | Base Rate | If a burglar is there what is the chance he chooses the front door? | 20% | |
| b | Base Rate | If a burglar is there what is the chance he chooses the back door? | 80% | |
| c | Forward | If the burglar chooses the front door, the chance of a break in? | 5% | |
| d | Forward | If the burglar chooses the back door, the chance of a break in? | 10% | |
| e | Forward | What is the chance the burglar breaks in from the front door? | a x c | (20% x 5%) = 1% |
| f | Forward | What is the chance the burglar breaks in from the back door? | b x d | (80% x 10%) = 8% |
| g | Forward | What is the chance a burglar breaks in on a given day? | e + f | 1% + 8% = 9% |
| h | Backward | If the burglar has broken in, what is the chance he came from the front door? | e/(e + f) | (1%)/(1% + 8%) = 11% |
| i | Backward | If the burglar has broken in, what is the chance he came from the back door? | f/(e + f) | (1%)/(1% + 8%) = 89% |
Observe the table above carefully and in the related diagram observe which edges do they correspond to. There are three things worth considering about backward probabilities from the table above.
- Backward Probabilities require information from all possible causes whereas Forward Probabilities do not: This is the key that makes backward probabilities difficult to calculate. Forward probabilities need information only about the immediate cause on which we have conditioned. However, backward probabilities need information on the likelihood of the effect from other causes as well to calculate the denominator.
- Backward Probabilities can be drastically different from analogous Forward Probabilities: Backward Probabilities can be very different from their forward probability counterparts. Note that the base rates of choosing the front door and the back door add new information to the backward probabilities.
- Backward Probabilities require at least two levels of information, there is no one level backward probability edge: Note that the backward probability edge necessarily needs the distribution over the different causes. This distribution in our case is the 20-80 (a,b) chance of selecting the front door and the back door. Without this distribution, it cannot mix the forward probabilities from different causes in the proper ratio.
Backward probabilities are structurally different from forward probabilities because they have to include the base rates of causes in calculations. Base Rates are close to the “priors” that the Bayesians have to define, without which their method does not work.

Conclusion
A discussion on the two types of probabilities is of importance in the study of statistical significance, because the question of significance can be posed in both directions as well. Frequentists usually pose this question as “Assuming there is no difference between the control and the variation, how extreme is the evidence against this hypothesis?”. Bayesians prefer to ask the question the other way round. “Having seen the evidence, what is the chance that the variation is equivalent to control?”. The philosophical question that follows is whether there is any difference of knowledge between the two types of questions or not. In practice, both often give the same answer.
In the next blogpost, I will introduce this debate between the Frequentists, the Bayesians and the Epistemologists and present VWOs perspective on the statistical debate.



