The Birth of Randomized Controlled Trials

Nature is a vicious genie designed to accurately answer all the questions she is asked, but still hide the truth from her inquirer in ingenious ways. A scientist is like a skilled interrogator trying to craft the right questions with his experiments to uncover the hidden truth. The genie is neither clear, nor consistent with her answers, but yes, she is a stickler for accuracy. She makes no effort at understanding the query the scientist has in his mind but yes, she accurately answers whatever she has been asked. She never lets him know when the question is inaccurately framed, and she quietly lets him celebrate his findings without uttering a word as he trods farther from the truth. And the game of science goes on as the difficulty was never in getting the genie to speak the truth, but always in framing the right question to ask.

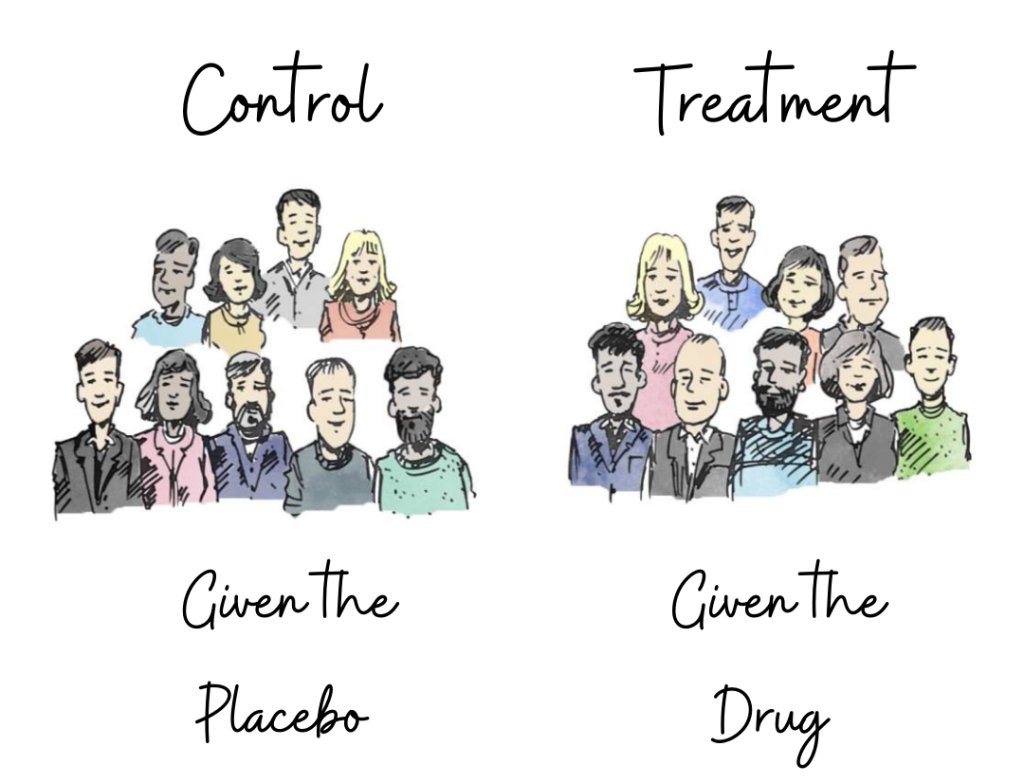
Let’s say a scientist wants to understand if a drug is helpful in reducing the fever of patients or not. He chooses two groups of patients and gives a placebo to one (the control) and the drug to the other (the treatment). An hour later, nature responds honestly by altering the temperature values in all patients. If the average temperature drops more for the treatment group than it did for the control, the scientist goes out to celebrate that his drug works. But what if the treatment group had a higher number of patients whose fever was already receding to start with? Alternatively, what if the control group had a higher number of patients who were more sick than those in the treatment? 

In reality, the scientist was not to compare the impact of the placebo on the control group with the impact of the drug on the treatment group. The right comparison would have been between the impact of the drug on the treatment group and the impact of the placebo also on the treatment group (the same set of patients). And this is the reason why it is so hard to frame the right experiment, because it is only possible to observe one outcome for one patient. The other outcome in strict scientific parlance is called the ‘counterfactual’. A counterfactual is essentially “what would have been if …”, the answer to which has always been and always will be unobservable.

The analogy above has been inspired by a beautiful passage written by Joan Fisher Box. She was neither a scientist nor a statistician but a writer. She was also the daughter of the man who gave birth to the randomized controlled trials in the 20th century, Ronal Aylmer Fisher. This blog post is about how Fisher solved the biggest problem in science and developed the procedure that powers all A/B tests today.

The Birth of Randomized Control Trials (RCT)

Randomized Control Trials (RCTs) is the statistical name of one of the most trustworthy approaches in experimentation that theoretically guarantees the cancellation of all other factors in an experiment. These “other factors” are also called confounders. The statistical definition of a confounder is a variable that affects both the cause and the effect of the study hence distorting the impact of the cause on the effect. It is an interesting story of how RCTs were invented and helps you grasp the intuition behind what confounders are, how they affect experiments, and how RCTs cancel out their impact.

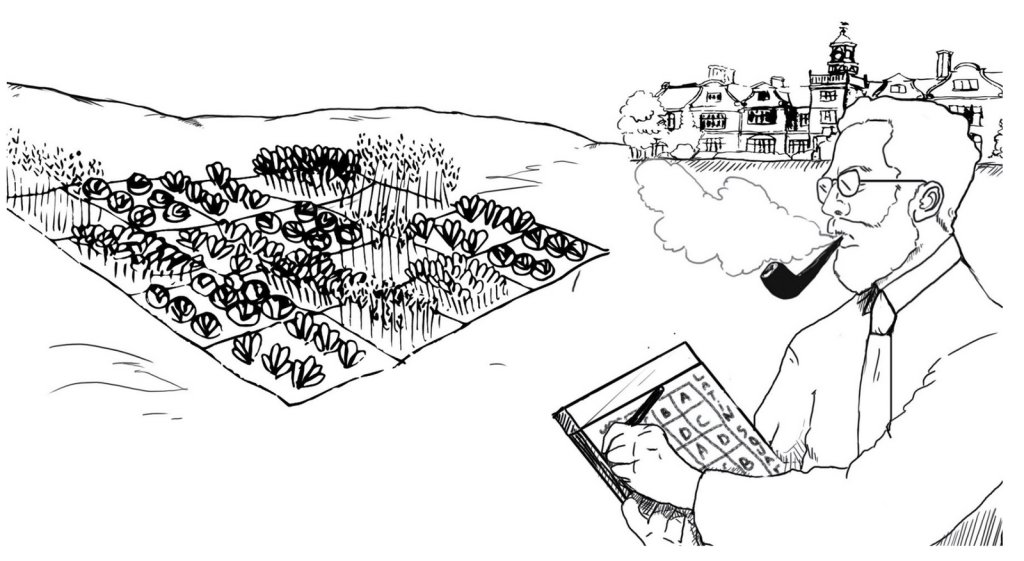
In the early 20th century, a scientist, R.A. Fisher wanted to study the impact of various fertilizers on the yield of his crops. Fisher started by neatly splitting his field into two parts and applying the fertilizer to only one. Fisher soon realized that reality was uncontrolled and random. The two halves of his land were different from each other in numerous regards. Both were receiving a different amount of sunlight, had a different soil quality, and also had variations in the water distribution (the confounders). With such vast differences in the underlying properties of the two halves, it was difficult to reliably estimate the impact the fertilizer was having.

To solve the problem, Fisher came up with an ingenious idea and in the process invented Randomized Control Trials (RCT), the holy grail behind modern experimentation. Fisher decided to neutralize the natural randomness in the environment by self-synthesizing randomness in his study.

Fisher divided his field into smaller squares and randomly chose the squares that would get the fertilizers and the ones that wouldn’t. This randomization ensured that all other factors affecting the yield were evenly divided between the ‘fertilizer’ and the ‘no fertilizer’ squares. The difference in the total yield of the two groups now revealed an unbiased estimate of the causal impact that the fertilizer was having on the yield.

And that was the birth of modern randomized experimentation that has majorly governed the scientific processes for the past 100 years. 

Randomization as the Secret Sauce

Fisher’s insight was phenomenal because he fought the war against randomness with randomness itself. Randomness complicates things but it still holds a hidden order that you can rely on. Imagine as a thought experiment, if you toss a fair coin 1000 times, it is likely to see 490 tails and 510 heads, but it is very unlikely to see 400 tails and 600 heads. In other words, randomness is bound to the law of large numbers and patterns emerge as the sample set becomes larger. This is the exact property that FIsher utilized to tackle the randomness of nature.

A perfect randomizer that randomly spits out 0s and 1s, correlates with nothing and hence evenly distributes all other attributes that might have been different in different parts of the field. The sunlight, the soil quality, and the water distribution all got evenly distributed in the two groups because theoretically they cannot be correlated to the coin toss in any way. Hence, Fisher was able to isolate the unique difference between the two groups, the one difference he artificially controlled – the fertilizer.

Conclusion

RCTs are the core statistical procedure that power all A/B testing today and randomization is the fundamental sauce that makes the procedure work. The vicious nature genie who has evaded revealing her true secrets forever since eternity stands dumbfounded in the face of Randomized Control Trials whenever the scientist is able to set it up correctly. But as history has it, randomization seems to be a simple concept but in practice very hard to implement. Computer scientists and philosophers have even gone on to claim that true randomness does not exist anywhere other than in Heisenberg’s uncertainty principle. What can be synthesized is only a close replica, which they call pseudo-randomness. 

The interesting ordeals of statistics are just getting started and I request the reader to hold on to the story without feeling desolate. In the end, all is fine, randomness does complicate the world we live in, but single-handedly grants it all the beauty it has.